毫米波干涉法测量结果及等离子体特征

在一个大气压下，一些针对低气压等离子体的诊断方法已不再适用。例如，在大气压下，两个最重要的等离子体参数——电子密度和温度不能用朗缪尔探针测量，因为电子平均自由程比德拜半径小。

微波干涉测量等离子体的折射率，已广泛应用于低气压等离子体的电子密度测量[35]。在低气压下，微波频率ω远大于等离子体频率ωpe和碰撞频率ν，即ω≫ωpe≫ν。在这种情况下，当微波穿过等离子体时，线平均电子密度与微波相移之间存在线性关系。然而，当ν≫ω≫ωpe时，对于高度碰撞等离子体，Laroussi报道电子数密度与相移有关，与碰撞频率相关[36]。当毫米波干涉仪系统用于诊断大气压等离子体的电子密度时，波频ω、等离子体频率ωpe和碰撞频率ν具有可比性，微波的相移及其振幅衰减由电子密度和碰撞频率所决定[37-39]。其相移系数和衰减系数可以表示为[37]

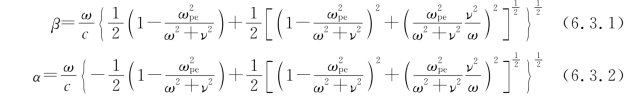
其中，c是真空中的光速。如果假设等离子体是均匀的，那么干涉信号的总相位变化Δφ和衰减ΔA可以通过下面的式子获得：

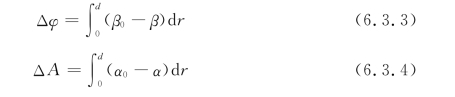
其中，β0和α0是自由空间值，d是等离子体的厚度。因此，根据测量所得的相移Δφ和衰减ΔA，可以从式（6.3.1）～式（6.3.4）中得到电子密度ne和碰撞频率ν。此外，碰撞频率是电子温度和碰撞截面的函数。因此，在一定条件下，也可以根据测量所获得的碰撞频率推算电子温度的信息。

这里采用105GHz毫米波干涉系统来测量大气压非平衡氦等离子体的电子密度和电子温度。等离子体由介质阻挡放电产生[40]。其中一个电极是由铝板覆盖的氧化铝片制成的。另一个电极由一个铜盘（直径5.7cm）制成，它有多个小孔，通过这些孔注入工作气体。孔的直径约为1mm，孔之间的距离为5mm，工作气体（氦）从孔中流入，进入放电间隙。间隙的距离固定为7mm。等离子体装置示意图如图6.3.1所示，高压脉冲发生器能够产生幅值达10kV的脉冲，脉冲宽度从200ns到直流，重复频率高达10kHz的脉冲直流方波[41]。本节将外加电压、脉冲宽度和脉冲频率分别固定在9kV、500ns和1kHz。电压脉冲的上升和下降时间约为100ns。由于外加电压的快速上升和下降时间，每个电压脉冲观察到两个不同的放电[40]。一次放电从施加电压脉冲的上升前沿开始，二次放电在施加电压脉冲的下降沿产生。关于电流和电压特性的详细信息可参考文献[40]。

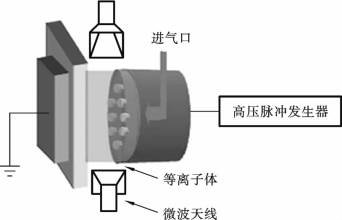
图6.3.1　放电系统示意图[41]

微波干涉测量系统的框图如图6.3.2所示。在等离子体关闭的情况下，通过将衰减器设置为最大衰减位置，同时打开Gunn振荡器，并测量两个混合器的直流电压输出来实现校准。其中一个混频器输出将作为I坐标，而另一个将作为笛卡尔坐标系中的Q坐标。这些测量将作为所有以下测量的参考点，然后将衰减器和移相器设置为零，当移相器进行360°的相位旋转时记录I、Q读数，当在I-Q图上绘制时，这些测量产生一个校准圆。

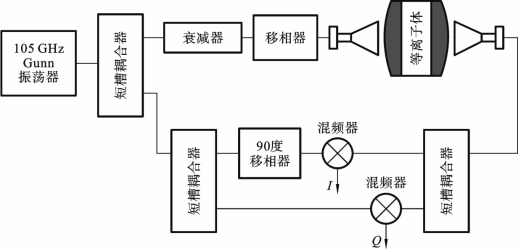
图6.3.2　微波干涉测量系统框图[41]

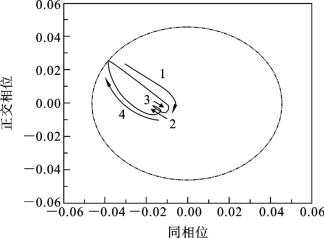
测量的I-Q曲线如图6.3.3所示，有等离子体时所得到的结果由实线表示，没有等离子体时的校准曲线由点划线表示。点划线的圆是校准圆，它是由移相器在没有等离子体的情况下通过整个旋转360°相位得到的。当等离子体产生时，毫米波同时经历相移和衰减，在图6.3.3中用实线表示。根据测量的相移和衰减，并通过式（6.3.1）～式（6.3.4）可以得到电子密度和碰撞频率，所得结果分别如图6.3.4和图6.3.5所示。在首次放电过程中，图6.3.4表明，电子密度在几十纳秒内增加到第一个峰值8×1012cm-3，此持续时间对应于图6.3.3中I-Q曲线的第1部分，其中毫米波表现出强烈的相移和衰减。然后电子密度在约430ns内衰减到4.1×1012cm-3，在此期间，波相移和衰减减小，对应于I-Q曲线的第2部分。

(www.xing528.com)

图6.3.3　I-Q关系图[41]

等离子体打开时得到的是实线曲线，等离子体关闭时得到的校准曲线用点划线表示

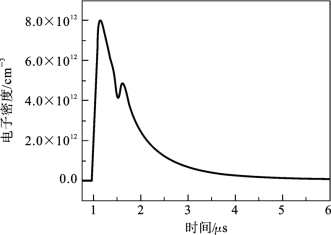
图6.3.4　测量所得到的电子密度随时间的变化曲线[41]

由于二次放电发生在外加电压脉冲的下降沿，电子密度再次增加。相应地，图6.3.3表明，在I-Q曲线第2部分之后，波形的相移和衰减在回到原始点之前再次增加（第3部分）。这个测量结果与放电的I-V特性是一致的，其中每个电压脉冲观察到两个不同的放电[40]。

图6.3.5给出了根据测量结果计算得到的碰撞频率随时间的变化曲线。有趣的是，在时间轴上碰撞频率具有与电子密度相似的行为。在高压下，主要的碰撞是在电子和中性粒子之间。碰撞频率ν可以表示为

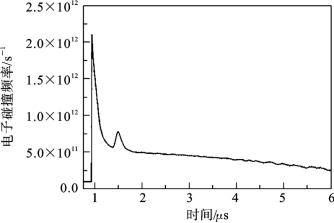
图6.3.5　测量所得电子碰撞频率随时间的变化曲线[41]

这里，n0、Te、me和σ0分别为中性粒子密度、电子温度、电子质量和电子中性碰撞截面，k是玻尔兹曼常数。由于气体温度接近室温，中性粒子密度n0可以被视为常数[40]。当Te低于10eV时，氦离子的碰撞截面几乎是一个常数[42]。因此，碰撞频率随时间的变化主要与电子温度有关。取σ0=5×10-20m2，然后可以根据氦粒子碰撞频率来估计Te[42]。图6.3.6给出了所得到的电子温度随时间的变化情况。在一次放电过程中，电子温度达到8.9eV的峰值，在2μs时衰减到大约0.5eV。应该指出的是，这里能够从测量的电子碰撞频率估算电子温度，是因为对于电子温度小于10eV，电子-氦气的碰撞截面几乎是一个常数。如果工作气体不是氦，比如是空气，那么从电子碰撞频率来计算电子温度将更加困难，因为氮/氧离子碰撞截面非常依赖于电子温度。

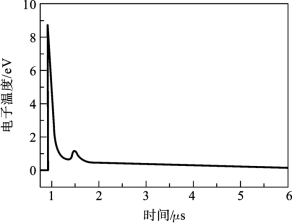
图6.3.6　测量得到的电子温度随时间的变化曲线[41]