能量交换是万有引力定律的根源

观察物体受热膨胀现象。

设A、B两物体质量分别为M、m，分别固定在相互平行的A、B平面，质心距为r。

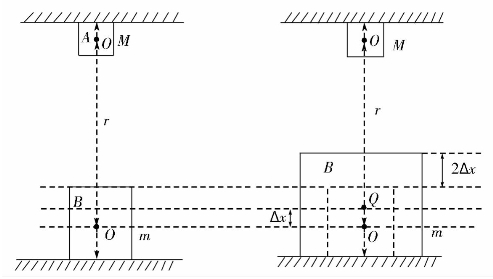
图1

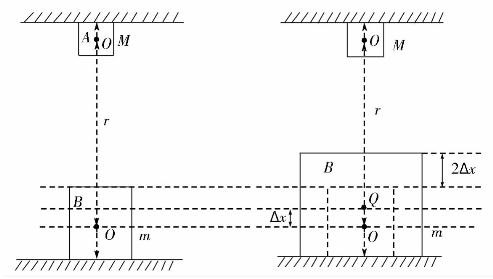
图2

图1是两物体在时间t为零的状态，图2是经过△t时间后，B物体受A物体辐射热能膨胀后的状态。

A向B辐射热能，B物体吸收使温度升高，经过△t后，B物体在A的一侧增大了2△x，即B物体的质心向A物体移动△x，质心从O点移动到Q点。

由运动定律：

S=Vt

即：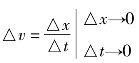

B物体在△t时间内，以速度△v向A物体运动△x。

由牛顿定律：

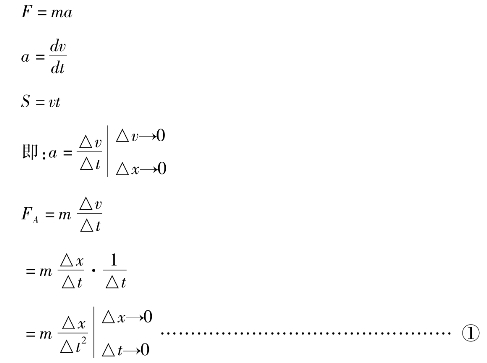
式中，FA为A施加给B的力、a为B向A运动的加速度。

设ρA为A物体单位质量辐射能量，A辐射总能量为：

EA=KA·ρA·M

式中：KA为A物体辐射有效系数。

则A在B处所具有的辐射能量密度ρ为：

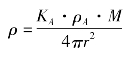
r为A、B质心距。

又设：α为单位时间内，B物体单位体积吸收的能量，(www.xing528.com)

v为B的体积，

δ为B单位时间内，在A、B质心连线上的膨胀长度。

则B物体质心移动的距离为：

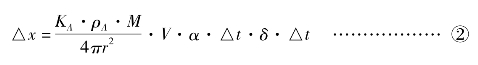
将②代入①，

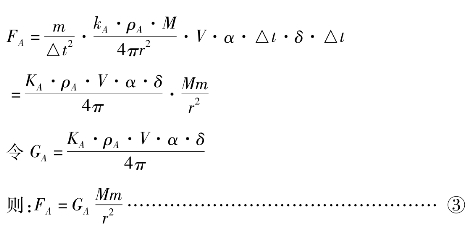
同理：可以求出B向A所施加的力。

A向B施加的力是由B指向A，而B向A施加的力是由A指向B，合力F为③式减④式：

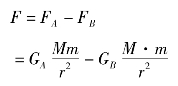
从⑤式看出，F为A、B两物体间常态下的作用力。

在自由空间，物体接受辐射能量，物体内部粒子相互作用加剧，便表现物体内部粒子带动整个物体向着受能方向的运动。这吸引物体运动的力应当就是通常所说的万有引力。

从广义角度说，引力应当起源于物体间的能量相互交换，这便是常态下的万有引力定律。

引力正比于质量，显然当给物体注入能量，其引力必将增加。

据质能关系E=mc2·即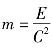，以此式乘以引力公式

即：（m′为相对应于注入质量）

令注入能量后物体的引力为F动，常态下为F常

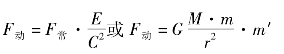
这便成了动态情况的万用引力定律。

这说明一个物体所具有的引力大小，正比于给这个物体注入的能量。