音乐数据分析：计算《京房六十律》的律数

在《后汉书·律历志》[128]中对“京房六十律”的生律方法进行了详细描述，在每一律的说明中指出了下一律的生律方法。如：“形始，十三万四千三百九十二。下生迟时。形始为宫，制时商，迟时徵。五日。律，六寸八分小分三弱。准，六尺八寸五千四百七十六。”这说明“形始”用“下生法”可以生成下一律“迟时”；又如“依行，十三万二千五百八十二。上生色育。依行为宫，谦待商，色育徵。七日。律，六寸七分小分三半强。准，六尺七寸七千五十九。”这说明“依行”用“上生法”可以生成下一律“色育”。表7-6是对所有“京房六十律”的生律顺序进行汇集。

表7-6　“京房六十律”的生律顺序与生律方法

观察表7-6，我们发现六十律的生律顺序可以分成以12个为单位的生律规律，后面的4个12律是按照第1个12律的生律方法进行重复生律的。即在表7-6中每行出现的是同样的生律方法。但是根据谷杰的研究发现，“谦待”“色育”的两律是不符合前面的生律规律的，即表7-6中第六行和第七行最后单元的斜体部分。

同时，除了初始律是由人指定的以外，其他五十九律都是用“上生法”或“下生法”按顺序依次得到，五十九律使用“上生法”总25次，使用“下生法”总24次。而在六十律的生律过程中，“上生法”或“下生法”的使用并不是一一交替出现的，那么其中的规律是什么，古人为什么要按这样的生律次序进行生律？这是值得研究的问题。[129]

“京房六十律”是以“三分损益法”为基础来生成六十律的，其中“上生法”即是“三分益一”，“下生法”即是“三分损一”，换句话说，“上生法”表明当前律是前一律乘以得到，“下生法”表明当前律是前一律乘以得到。当“黄钟”律的律数是9时，它的下一律“林钟”的律数由“黄钟”按“下生法”得到，即9×=6，“林钟”的下一律“太簇”的律数由“林钟”按“上生法”得到，即6×=8，以此类推，可得到所有六十律的律数。具体算法过程如下：

根据上述算法过程可以计算出各律律数，它的Matlab建模代码见附录【代码7-1】。

缪天瑞在《律学》第117页写道：

京房在计算律时用了三个数字，一是实数，二是律数，三是准数。这里的实数是3的11次方等于177147，为黄钟的实数，然后用此数按三分损益上下相生得其余五十九律的实数。将各律的实数分别除以19683，所得的商数以寸、分、小分为名的数，即律数。除不尽时用强或弱来表示。所得之商数以尺、寸为名的数，即准数，亦京房律准上弦振动部分的长度，寸位后除不尽的余数照录。[130]

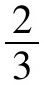由于一般人为指定的出发律都为整数，也可以表示为分数，如81，就是，而“三分损益法”的方法是乘以或。如果用分数表示律数，若前一律为，则用“上生法”得到下一律就是，用“下生法”得到下一律就是，这样下一律仍然是分数式。同时，用“上生法”或“下生法”得到下一律，分母都要乘以一个3，而分子则乘以2的2次或2的1次，用公式表示第i个律的律数计算公式为：

k是需要生律的数量，f1是出发律（也叫起始律），常见的出发律有f1=9或81或177147。

根据表7-6的“上生法”或“下生法”使用序列，对公式（7-1）中的分子和分母进行列表说明，得到表7-7。表7-7中包含有各律的律名，生律次序，分子的2的幂次f（i）。

表7-7　“京房六十律”分数式的分子分母的幂次

在整个生律序列中，所有六十律在公式（7-1）中的分母构成一个等比数列，即是以3为底的等比数列X=[30，31，32，……，359]，而在公式（7-1）中的分子则是以2为底的非等比的幂数列f（i）=[0，1，3，4，6，7，9，11，12，14，15，17，19，20，22，23，25，26，28，30，31，33，34，36，38，39，41，42，44，45，47，49，50，52，53，55，57，58，60，61，63，64，66，68，69，71，72，74，76，77，79，80，82，84，85，87，88，90，91，93]，幂次最小值为0，最大值为93，相邻两律的幂次相差1或2。

对生律序列中各律的幂次f（i）序列进行图示，得到图7-3。如图7-3所示，离散的各点是按生律序列提升的，分数式的分子幂次是拟线性增长的。

图7-3　“京房六十律”分数式的分子幂次(www.xing528.com)

接着，在图7-3上加画出如下拟合直线的各离散点，得到图7-4，“京房六十律”分数式的分子幂次的拟合直线为：

在图7-4中，拟合直线的离散点为圆圈，分子幂次的离散点为圆点，观察图7-4发现，拟合直线与分数式的分子幂次非常接近。为了分析方便，在此画出了g（i）～f（i）的离散点，得到图7-5。观察图7-5得知，所有离散点的Y轴值不超过1，大于-0.5，同时这些散点呈现右下和左上方向平行的特点，左上方向为6个散点为一组组成一条直线，右下方向为11个散点为一组组成一条直线。

为了能求出任意指定小数位数的“京房六十律”律数，我们重新对生律过程进行建模，建模过程如下：

图7-4　“京房六十律”分数式的分子幂次的拟合直线

图7-5　“京房六十律”分数式的分子幂次的拟合直线与分子幂次的差

（1）用数组来表示长整数，其中数组第1个元素存储长整数的个位数，第2个元素存储长整数的百位数，以此类推。

（2）计算出“京房六十律”分数式的分子和分母，分别用两个二维数组fz和fm表示，二维数组的第i行表示第i个律的长整数分子或分母，分别记为fz（i）或fm（i）。

（3）利用两个长整型数fz（i）和fm（i），分别做分子和分母，针对指定的小数位数k，计算出第i个律的律数，k位小数的律数用长整数表示。

在上述建模过程的第（2）步中，由于待求律的长整数分子fz（i）是前一律长整数分子fz（i-1）乘以2或4得到，待求律的长整数分母fm（i）是前一律长整数分母fm（i-1）乘以3得到，因此需要设计计算长整数乘以个位数2或3或4的算法，结果为长整数。算法如下：

利用此算法可以得到fz（i）和fm（i），结果见表7-8。

表7-8　“京房六十律”公式（7-1）的分数式的分子和分母值

当出发律黄钟的律数是9时，利用表7-8可以计算出“京房六十律”各律的律数，表7-9为“京房六十律”小数点后50位的计算结果。

表7-9　“京房六十律”的50位小数计算结果