中国古代的音律实践源远流长，七千多年前的西安半坡村仰韶文化遗址和浙江杭州湾河姆波遗址中出土的陶埙能发出小三度音程，湖北随县（今随州市）出土的2500多年前的曾侯乙编钟有完整的音律体系。[120]
有关音律计算的实践最早记录在成书于公元前五世纪的《管子·地员篇》：
凡将起五音，凡首，先主一而三之，四开以合九九，以是生黄钟小素之首，以成宫。三分而益之以一，为百有八，为徵。不无有三分而去其乘，适足以是生商。有三分而复于其所，以是成羽。有三分去其乘，适足以是成角。[121]
上述音律计算的方法称为“三分损益法”，由“三分损益法”产生的音律称为“三分损益律”，“三分损益法”成为了古代中国主流的音律生律方法，频繁出现在中国历代音乐研究文献和官方的各种律历志中。[122]
由“三分损益法”生成十二音阶的各音律的方法记录于公元前三世纪秦朝时期的《吕氏春秋·音律篇》中：
黄钟生林钟，林中生太簇，太簇生南吕，南吕生姑洗，姑洗生应钟，应钟生蕤宾，蕤宾生大吕，大吕生夷则，夷则生夹钟，夹钟生无射，无射生仲吕。三分所生，益之一分以上生；三分所生，去其一分以下生。黄钟、大吕、太蔟、夹钟、姑洗、仲吕、蕤宾为上；林钟、夷则、南吕、无射、应钟为下。[123]
由此，在中国秦朝以后的音律研究中，“上生”和“下生”分别表示了两种不同的音律生成方法，如在《淮南鸿烈·天文训》《京房六十律》《钱乐之三百六十律》《万宝常一百四十四律》《蔡元定十八律》及各代《律历志》均利用或参照“三分损益法”生成音律，成为了中国古代最主要的生律方法。[124]
“三分损益法”从第一律出发，按“上生”和“下生”方法逐个生成音律，每一个新律是由前一律生成，这样前后相连的生律法生成的音律是有序的，我们称“三分损益法”为“链式生律法”，生成的各律构成音律序列。(www.xing528.com)
中国古代的音律研究者，一般都先指定第一个出发律（也叫始发律）的律数，然后按照确定的“上生”和“下生”方法逐个生成音律。如《管子·地员篇》中的“宫”为81，“上生”得“徵”为108。
中国汉代刘安（前179—前122）编写的《淮南鸿烈》中记录了十二律的生成方法：“以黄钟为宫，其数八十一，下生林钟，林钟之数五十四，上生太蔟，太蔟之数七十二，下生南吕，南吕之数四十八，上生姑洗，姑洗之数六十四，下生应钟，应钟之数四十二，上生蕤宾，蕤宾之数五十七，上生大吕，大吕之数七十六，下生夷则，夷则之数五十一，上生夹钟，夹钟之数六十八，下生无射，无射之数四十五，上生仲吕，仲吕之数六十。”
中国史学家司马迁（前145—前89）的《史记·律书》在计算“三分损益律”时，采用了分数的形式，他设黄钟（C）的律数为1，则其他十一律的律数全是分数。“子一分，丑三分二。寅九分八。卯二十七分十六。辰八十一分六十四。巳二百四十三分一百二十八。午七百二十九分五百一十二。未二千一百八十七分一千二十四。申六千五百六十一分四千零九十六。酉一万九千六百八十三分八千一百九十二。戊五万九千四十九分三万二千七百六十八。亥十七万七千一百四十七分六万五千五百三十六。”
《后汉书·律历志》记录有西汉律学家京房（前77—前37）答官员问，曰：“六十律相生之法：以上生下，皆三生二；以下生上，皆三生四。阳下生阴，阴上生阳，终于中吕，而十二律毕矣。中吕上生执始，执始下生去灭，上下相生，终于南事，六十律毕矣。夫十二律之变至于六十，犹八卦之变至于六十四也……《礼运篇》曰：‘五声、六律、十二管还相为宫’，此之谓也。”京房以黄钟律为出发律，利用“三分损益法”推演到了六十律，以符合“十二管还相为宫”的目的。
《隋书·律历志》记载：“宋元嘉中（424—453），太史钱乐之因京房‘南事’之余，引而伸之，更为三百律；终于“安运”，长四寸四分有奇；总合为三百六十律。”钱乐之利用“三分损益法”推演了三百六十律，并发现了与出发律最近的“安运”律。此外，《隋书·律历志》还记录了中国南北朝时何承天（370—447）创制的一种新律：“承天更设新率，则从中吕还得黄钟。十二旋宫，声韵无失。”何承天把“三分损益法”推算出的第十二律与出发律的误差平均分配到各律中，他的生律新法被音乐史学家称为十二平均律的近似方法。在《旧五代史·乐志》中记载有王朴先利用“三分损益法”生律时，通过调整分母的方法求出前三律，再利用“三分损益法”求出其他律。南宋蔡元定（1135—1198）在其《律吕新书》中提出了十八律的理论，其十八律也采用“三分损益法”为生律法。
到了明代，朱载堉发明了十二平均律，在其所著的《律历融通》中，记录了利用“三分损益法”的基本思想，通过调整“三分损益法”分数式中分母数的方法，计算十二平均律的律间比例常数，即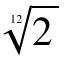
，再利用这个比例常数从指定的出发律开始逐个计算出各律。
到20世纪，陈其翔等利用多位小数分数逼近法来生成“三分损益法”的各律，此方法可得到误差越来越小的生律次数及其误差的音分值。多位小数分数逼近法分三步：①先确定两个分数，两个分数比被逼近的给定小数P，一个大，称A，一个小，称B；②把A和B的分子和分母分别相加，得到新的分数C，若C大于P，则C赋值给A，否则赋值给B；③如果C的精度符合预定要求，则停止，否则，继续运行②。[125]
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
