乐队指挥手势识别-音乐数据分析

乐队指挥是一个乐队的灵魂，是乐曲演奏中速度控制、情绪控制、乐器控制和制约其他音乐信息的核心，乐队指挥主要依靠双手和面部表情把信息传递给乐队的每个成员，每个成员根据乐队指挥的信息演奏自己的声部，满足和服从整体乐曲演奏的情感需求和节奏要求。

乐队指挥的双手在乐曲的进行中，不断在三维空间运动，带给乐队大量的乐曲信息，其中最基本的信息是节奏信息。节奏信息中节拍是乐曲表达的主要信息之一，不同的节拍对应不同的双手动作，节拍决定了乐队指挥双手的基本运动轨迹。如2/4拍的乐曲，双手的基本运动轨迹是对称地按“∞”形从内到两侧连续运动，而3/4拍的乐曲，双手的基本运动轨迹是对称地按“正三角形”不断运动。

从Kinect的骨骼关节坐标系分析，乐队指挥2/4拍和3/4拍的打拍轨迹在三维空间的X、Y、Z轴上运动方向有所不同，如表6-6所示为不同节拍在Kinect坐标的运动方向。

表6-6　乐队指挥2/4拍和3/4拍的打拍轨迹的Kinect坐标运动方向分析

这一节，将根据第二章的数据获取方法，利用Kinect得到基本的乐队指挥的2/4拍和3/4拍的运动关节数据，然后根据运动关节数据对这两个不同拍号进行分类。先获取动作模板库，分别得到2/4拍和3/4拍的一个完整指挥动作的若干个分解动作组成模板库；然后对未分类的一个完整指挥动作，利用DTW算法计算和模板库中所有动作的最小累积值，根据最近邻法在这些值中找到最小的一个累积值，把此未分类的动作归到此节拍动作中。

一、关节动作分割

乐队指挥的2/4拍和3/4拍的动作运动轨迹，在人眼中是较固定周期、连续不断反复的。利用Kinect得到的动作数据是连续的时序数据，首要的任务是对这些连续的时序数据进行分割，得到每个周期的动作数据，一个动作周期的运动数据构成一个数据组，这个数据组是节拍识别的特征数据。

由于乐队指挥双手的动作以手腕关节的运动最为明显，同时，乐队指挥的双手在通常情况下是对称运动的，所以这里利用Kinect采集右手手腕关节的数据，然后利用“自适应迭代平滑分割算法”[119]对运动数据进行分割。分三个步骤：①求平滑步长：利用自相关函数求出关节运动数据的自相关系数，然后设定自相关系数为平滑步长；②迭代平滑：“自适应迭代平滑分割算法”利用此平滑步长对采集的运作数据进行循环迭代平滑，然后根据拐点数的变化进行平滑控制；③数据分割：根据各个拐点对采集的运动数据进行分割，得到每个周期的动作数据。

1.求平滑步长

乐队指挥的右手手腕关节的三维空间运动是循环反复的，采集的数据也有周期性，也就是说，对于三维空间的每一维时序数据，存在一定的自相似性；同时，由于任意两个周期内的数据个数可能不同，对应位序上的数据也会存在一定的偏差，时序数据的分割不能为简单的等长分割。由于每一维的时序数据都存在一定的自相似性，所以可以利用时间序列的自相关系数得到整体上的移位最佳相似度，这个移位步长就是平滑步长。

对于两个时序序列而言，序列在时间维度上的变化可能有一定的相关程度，相关系数是用以反映时间维度上两个序列之间关系密切程度的统计指标；两个时序序列X和Y的相关系数计算方法如下：

其中σ（X）和σ（Y）分别表示X和Y的标准差，Cov（X|Y）表示X和Y的协方差。

自相关是指某时序序列于其自身移位后在不同时间点的相关程度。假设原始时序序列为X，共有n个元素，表示为：X={x1，x2，……，xn}，移位步长为w后序列X的自相关系数就是计算两个时序序列{x1，x2，……，xn-w}和{xw+1，xw+2，……，xn}的相关系数。计算公式如下：

其中μ表示X的标准差，w表示滞后时间，t表示时间变量。

由于移位步长w可以是1～n-1，所以需要计算n-1个不同的自相关系数ρ，而不同的自相关系数ρ说明不同的含义，一般而言，相关系数的绝对值在0.8～1.0范围表示极强相关，在0.6～0.8范围表示强相关，在0.4～0.6范围表示中等程度相关，在0.2～0.4范围表示弱相关，在0.0～0.2范围表示极弱相关或无相关。

由于乐队指挥的动作具有周期性，因此动作时序数据的自相关系数在不同的移位步长下有不同的值，也会表现出极强相关或强相关的情况，下面利用Matlab的自相关函数计算利用Kinect获取的乐队指挥的动作时序数据的自相关系数。Matlab代码如下：

运行上述代码，可以得到如图6-4所示结果。

图6-4　乐队指挥3/4拍右手手腕关节X、Y、Z轴运动时序数据的自相关系数

随着位移步长w的增大，右手手腕关节X、Y、Z轴运动时序数据的自相关系数值在数轴y=0处上下波动，右手手腕关节X、Y、Z轴时序数据的波动一致，在步长w轴上，自相关系数值的波动具有一定的周期性，这反过来说明乐队指挥的动作具有重复周期性。

自相关系数处于强相关范围的位移步长是最能体现周期性的，因此设定平滑步长w为图中第1次和第2此自相关系数由正转负的点之间的w轴的差的一半。实现Matlab代码如下：

运行上述代码，可以得到如图6-5所示结果，图中的X轴是图6-4中的X曲线的数值由正变负时，所有转折点的序号；Y轴是相邻的前后两个转折点的位移差，图中位移差的变化由稳定到微小波动再到剧烈波动，充分体现了随着位移的增大，总体上自相关由强到弱的变化。

图6-5　乐队指挥3/4拍右手手腕X轴运动时序数据的自相关系数位移差

如图6-5所示，第1个圆点对应的位移差是72，也就是说，当位移为72时，运动数据的自相关性最大，由于Kinect获取骨骼帧数据是每秒30帧，所以大约可以估计乐队指挥3/4拍的打拍周期是72/30=2.4秒左右，按上面的设定原则，可以得到平滑步长w为72/2=36。

2.迭代平滑

得到平滑步长w后，利用自适应迭代平滑分割算法对运行时序数据进行分割，它需要对数据进行平滑操作和拐点计数，如果相邻两次平滑后，数据的拐点数相同，那么迭代平滑结束。

平滑操作的Matlab函数代码如下：

拐点计数的Matlab实现函数如下：

利用上述代码，对乐队指挥的3/4拍动作的右手手腕关节的X轴数据迭代平滑运行20次，可以得到如图6-6和图6-7所示结果。

图6-6　乐队指挥右手手腕关节运动X轴数据迭代平滑20次结果

图6-7　乐队指挥右手手腕关节运动X轴数据平滑次数与拐点数的关系

如图6-6所示，数据在迭代平滑过程中，各次平滑后的数据逐步向中间曲线逼近，各个“山峰”或“山谷”表现出明显的周期性。如图6-7所示，原始数据的拐点数达到近700，迭代平滑后，拐点数逐步降低，特别是第1次平滑后拐点数下降很明显，然后缓慢下降。

调用两个函数的代码如下：

3.数据分割

数据分割的目的是将数据按周期性动作进行分割，使得分割后的每段数据为乐队指挥的一个完整3/4拍的动作数据。

利用自适应迭代的算法思想，只要在迭代平滑过程中，相邻两次的拐点数相等，迭代平滑就停止。按此思想，如图6-8所示，前6个拐点数分别为：698，76，60，57，57，57，除第1个698是原始数据的拐点数外，在第3次和第4次平滑后的拐点数都是57，所以迭代到第4次后，平滑就结束。(www.xing528.com)

图6-8　乐队指挥右手手腕关节运动X轴数据分割结果

第4次迭代平滑后，利用上述代码函数可以得到每个拐点在时间轴上的分割坐标值（IPArr数组），利用数组标记值（向上转折标记值为1，向下转折标记值为0）为0的坐标值对乐队指挥右手手腕关节运动x轴数据进行分割。

具体的画图过程由几个函数构成，分别是自适应迭代平滑分割函数、分割线坐标获取函数和画图函数组成，这些函数代码如下：

其中，自适应迭代平滑算法得到平滑后最终数据的函数如下：

而求出分割线的函数代码如下：

运行上述代码，可以得到如图6-8所示的对右手手腕X轴的时序数据分割结果。大多数虚线都处于原始数据的“山谷”部分，能较好地分割原始数据。

二、基于DTW和K最近邻法的节拍识别

动态时间规整算法（DTW）是衡量两个时序序列相似度的度量方法，它能得到两个时序序列之间的最小累积值，具体实现方法在上文章节中已经进行详细描述，这里利用它来度量两个动作的数据序列之间的相似度。

K最近邻（KNN, K-Nearest Neighbor）分类算法是模式分类技术中最简单的方法之一。所谓K最近邻，就是K个最近的邻居的意思，说的是每个样本都可以用它最接近的K个邻居来代表。KNN算法的核心思想是如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。此方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

乐队指挥的动作数据的节拍识别是对Kinect获取的关节数据进行模式分类，确定乐队指挥的动作属于哪类节拍的过程。

1.节拍识别的步骤

（1）假设节拍的种类是有限，且在某具体实例中，分类对象由已知的若干个单拍子组成；音乐乐曲的节拍众多，常见的像2/4、3/4、4/4、6/8等单拍子，还有很多混合拍子，这些拍子有着相对固定的指挥模式，如3/4拍是左右手按“三角形”对称运动，在所有3/4拍乐曲中，运动轨迹相对固定，按周期反复。

（2）节拍模板库获取，对已知的若干个单拍子分别进行运动数据获取，不同两次获取数据时，与设备的初始距离不同，所以对每次运动时序数据的三维坐标值，减去它们的均值，实现函数代码如下：

然后利用上述的数据分割方法，对每个不同拍子的动作数据进行分割，分割为一组一组的时序数据，每组数据属于单周期的拍子动作轨迹，这些数据组构成节拍模板库，并为模板库中的每个模板标记节拍拍号，为待分类节拍数据的分类提供匹配对象，假设模板库中有k种节拍，每种节拍分别有mi（1≤i≤k）个模板，这样模板库中共有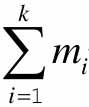个模板。

（3）利用DTW计算某一待分类节拍与节拍模板库所有模板的相似度，当获取某一待分类节拍的动作运动轨迹数据后，首先对运动轨迹数据进行数据分割，按周期分割为几组数据，假设为d组，然后利用DTW对待分类节拍的d组数据的每组与模板库中的所有模板进行相似度度量，分别计算X、Y、Z轴的相似度，一共可以得到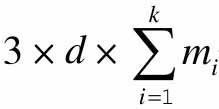个比较结果。

（4）利用K最邻近法对此待分类节拍进行分类，对待分类节拍的d组数据，每组数据与模板库中所有模板计算DTW相似度，得到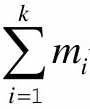个相似度结果，求出这些相似度中最小的相似度，此模板对应的节拍标记就作为此组待分类节拍数据的节拍，待分类节拍的d组数据得到3×d个分类结果。

（5）计算节拍分类识别率，统计3×d个分类结果中正确分类的个数，假设为c个，那么分类识别率为c/（3×d）。

2.实验结果

这里假设需要分类的乐队指挥的节拍为2/4拍和3/4拍两类，利用Kinect分别获取了乐队指挥的三次打拍动作轨迹数据，对应2/4拍、3/4拍和2/4拍，以第1次和第2次获取的2/4拍和3/4拍的动作数据为模板数据，第3次获取的2/4拍的动作数据为待分类数据。

具体分类步骤如下：

（1）数据分割，利用上述数据分割方法对获取到的2/4拍和3/4拍的动作轨迹数据进行分割，取第1次和第2次的2/4拍、3/4拍分割后的单周期数据作为动作模板库，记为A1、A2，把第3次的2/4拍动作轨迹数据分割后的单周期数据作为待分类数据，记为B。

实验获取的节拍动作轨迹时序数据A1、A2和B分别分割为28、14、31个周期数据。

（2）利用DTW算法分别计算B中每个数据组的X、Y、Z轴数据和A1、A2中所有模板进行相似度度量。

计算过程由两个函数构成，分别是计算两个单周期时序数据序列的DTW相似度的函数（见第二章）和计算两个节拍动作轨迹的时序序列的DTW相似度的函数，计算两个节拍动作轨迹DTW相似度函数的代码如下：

（3）根据最近邻法求出所有B中的每组时序数据的分类结果，计算总的识别率。对于B中的每组时序数据b，它包含有X、Y、Z三维的数据，它们分别与模板库A1和A2中的每组时序数组的X、Y、Z三维数据进行DTW相似度度量，然后根据最近邻法找出A1或A2中的最小DTW相似度，如果最小值在A1，那么认为B的这组时序数组的X或Y或Z维度上属于A1类别（即2/4拍），反之，属于A2类别（即3/4拍）。

判断代码如下：

上述代码先利用ComputerDTW函数计算两个节拍动作轨迹的DTW相似度，再分别在A1和A2中找出最小值，比较这两个最小值，然后分别进行分类标记（1或2），最后输出结果。

对实验中采集的2/4拍和3/4拍数据，分类的结果如表6-7所示。

表6-7　乐队指挥的2/4拍待分类动作对2/4拍和3/4拍动作模板库分类结果

分类结果是1表示B的此组时序数据的X、Y、Z轴分类到A1类，分类结果是2的为A2类，由于B是2/4拍的打拍运动轨迹，而A1和A2分别是2/4拍和3/4拍打拍动作轨迹，所以分类结果1表示分类正确，对表6-7的统计结果，统计代码如下：

统计结果如表6-8示。

表6-8　乐队指挥2/4拍打拍运动轨迹分类结果统计

Kinect获取的乐队指挥2/4拍打拍的运动轨迹的X轴数据作为特征的识别率最高，其次是Y轴，最低是Z轴，31组待分类时序数据的平均分类正确率为53.76%。