【主要内容】
1.假设检验的概念
为了对总体X的分布的未知参数作出推断,先提出一个与要推断的结论有关的假设H0(称为原假设)以及与之对立的假设H1(称备择假设),然后在H0为真的条件下,通过选取适当的统计量构造一个小概率事件.将来自X的一个简单随机样本的观察值代入这个统计量,如果上述的小概率事件发生了,就拒绝H0,接受H1;否则接受H0.这个决策过程称为假设检验.
2.一个正态总体的参数的假设检验
设总体X~N(μ,σ2),X1,X2,…,Xn是来自X的一个简单随机样本,且记样本均值为X,方差为S2.
(1)当σ2已知时,μ=μ0的显著性水平为α(0<α<1)的假设检验为:H0:μ=μ0,H1:μ≠μ0,
检验统计量 (将样本观察值代入后的Z记为z),拒绝域z≥zα/2.
(将样本观察值代入后的Z记为z),拒绝域z≥zα/2.
(2)当σ2未知时,μ=μ0的显著性水平为α(0<α<1)的假设检验为:H0:μ=μ0,H1:μ≠μ0,
检验统计量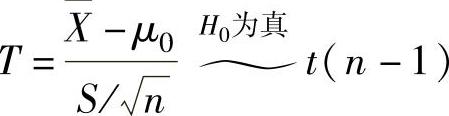 (将样本观察值代入后的T记为t),拒绝域|t|≥tα/2(n-1).
(将样本观察值代入后的T记为t),拒绝域|t|≥tα/2(n-1).
(3)当μ未知时,σ2=σ02的显著性水平为α(0<α<1)的假设检验为:H0:σ2=σ02,H1:σ2≠σ02,
检验统计量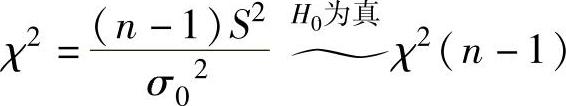 (将样本观察值代入后的χ2仍记为χ2),拒绝域χ2≤χ21-α(n-1)或χ2≥χ2α(n-1).
(将样本观察值代入后的χ2仍记为χ2),拒绝域χ2≤χ21-α(n-1)或χ2≥χ2α(n-1).
3.两个正态总体的参数的假设检验
设总体X~N(μ1,σ12)和Y~N(μ2,σ22),X1,X2,…,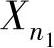 和Y1,Y2,…,
和Y1,Y2,…,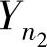 是分别来自X和Y的简单随机样本,它们相互独立,且记X1,X2,…,
是分别来自X和Y的简单随机样本,它们相互独立,且记X1,X2,…,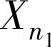 的均值为
的均值为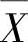 ,方差为S12;Y1,Y2,…,
,方差为S12;Y1,Y2,…, 的均值为
的均值为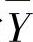 ,方差为S22.
,方差为S22.
(1)当σ12,σ22已知时,μ1-μ2=δ的显著性水平为α(0<α<1)的假设检验为H0:μ1-μ2=δ,H1:μ1-μ2≠δ,
检验统计量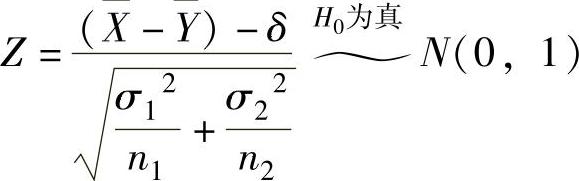 (将样本观察值代入后的Z记为z),拒绝域z≥zα/2.
(将样本观察值代入后的Z记为z),拒绝域z≥zα/2.
(2)当σ12=σ22=σ2,但σ2未知时,μ1-μ2=δ的显著性水平为α(0<α<1)的假设检验为:
H0:μ1-μ2=δ,H1:μ1-μ2≠δ,
检验统计量 (将样本观察值代入后的T记为t),拒绝域|t|≥tα/2(n1+n2-2).
(将样本观察值代入后的T记为t),拒绝域|t|≥tα/2(n1+n2-2).
(3)当μ1,μ2未知时,σ12=σ22的显著性水平为α(0<α<1)的假设检验为:H0:σ12=σ22,H1:σ12≠σ22,
检验统计量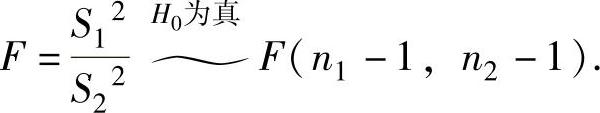
拒绝域F≤F1-α/2(n1-1,n2-1)或F≥Fα/2(n1-1,n2-1).
4.两类错误
参数的假设检验中会犯两类错误:第Ⅰ类错误和第Ⅱ类错误.
当原假设H0为真时,作为拒绝H0的决策的错误,称为犯第Ⅰ类错误(也称弃真错误).当原假设H0不真时,作出接受H0的决策的错误,称为犯第Ⅱ类错误(也称取伪错误).显然
P(犯第Ⅰ类错误)=P(拒绝H0|H0为真)=α(α是显著性水平)(https://www.xing528.com)
P(犯第Ⅱ类错误)=P(接受H0|H0不真).
【典型例题】
例8.6.1 设某次考试的考生成绩服从正态分布,从中随机抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平α=0.05下,是否可认为这次考试的考生平均成绩为70分.
精解 记考生成绩为X,则X~N(μ,σ2).
现在的问题是在σ2未知时检验μ=70.具体如下:
H0:μ=70,H1:μ≠70,
检验统计量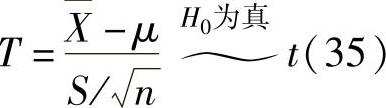 (将样本观察值代入T后记为t)
(将样本观察值代入T后记为t)
拒绝域|t|≥tα/2(n-1)=t0.025(35)=2.0301.
将μ=70,x=66.5,s=15,n=35代入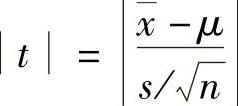 得|t|≈1.4,显然它不在拒绝域内,所以接受H0,可认为这次考试的考生平均成绩为70分.
得|t|≈1.4,显然它不在拒绝域内,所以接受H0,可认为这次考试的考生平均成绩为70分.
例8.6.2 设总体X~N(μ1,σ12),Y~N(μ2,σ22),μ1,μ2未知,X1,X2,…,Xn与Y1,Y2,…,Yn是分别来自X与Y的简单随机样本,且相互独立,记它们的方差分别为S12与S22,试写出检验假设
的统计量及拒绝域(已知显著性水平为α).
精解 由于是在μ1,μ2未知的情形下,检验假设
H0:σ12=σ22,H1:σ12≠σ22,
所以使用统计量为
拒绝域为 F≤F1-α/2(n-1,n-1)或F≥Fα/2(n-1,n-1).
例8.6.3 某工厂生产一种螺钉,标准要求长度为68(mm),实际生产的产品的长度服从正态分布N(μ,3.62).考虑假设检验:
H0:μ=68,H1:μ≠68.记X是样本均值.按以下方式进行假设检验:
当|X-68|≤1时,接受H0;当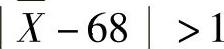 时,拒绝H0.
时,拒绝H0.
(1)当样本容量n=36时,求犯第Ⅰ类错误的概率α;
(2)在μ=70,n=64时,求犯第Ⅱ类错误的概率β.
(2)现在的统计量为
所以,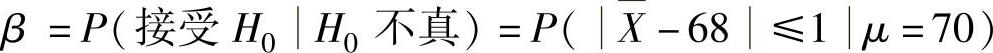
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




