正态总体参数的区间估计方法

【主要内容】

1.区间估计的概念

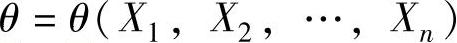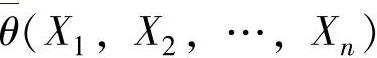设θ是总体X的未知参数，X₁，X₂，…，X_n是来自X的简单随机样本.θ的区间估计就是对给定的实数α（0<α<1），根据样本构造两个统计量和，使得

则称（θ，θ）为置信度是1-α的置信区间.这种用置信区间估计未知参数的方法称为参数的区间估计.

2.一个正态总体未知参数的区间估计

设X₁，X₂，…，X_n是来自正态总体X～N（μ，σ²）的一个简单随机样本，X为样本均值，S²为样本方差.

（1）当σ²已知时，未知参数μ的置信度为1-α的置信区间为

（2）当σ²未知时，未知参数μ的置信度为1-α的置信区间为

（3）当μ未知时，未知参数σ²的置信度为1-α的置信区间为

3.两个正态总体未知参数的区间估计

设X₁，X₂，…，X_m为来自正态总体X～N（μ₁，σ₁²）的一个简单随机样本，X为样本均值，S₁²为样本方差；设Y₁，Y₂，…，Y_n为来自正态总体Y～N（μ₂，σ₂²）的一个简单随机样本，为样本均值，S₂²为样本方差，且两个总体相互独立.

（1）当σ₁²，σ₂²已知时，未知参数μ₁-μ₂的置信度为1-α的置信区间为

（2）当σ₁²=σ₂²=σ²，但σ²未知时，未知参数μ₁-μ₂的置信度为1-α的置信区间为

（3）当μ₁，μ₂未知时，未知参数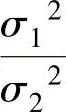的置信度为1-α的置信区间为

【典型例题】

例8.5.1 （单项选择题）设总体X～N（μ，σ²），其中μ，σ²未知，X₁，X₂，…，X_n是来自X的简单随机样本，它的均值与方差分别为X和S²，则_μ的置信度为1-α的置信区间为（ ）.

精解 在σ²未知时，μ的置信度为1-α的置信区间为

因此本题选B.(www.xing528.com)

例8.5.2 （单项选择题）设总体X与Y相互独立，X～N（μ₁，σ₁²），Y～N（μ₂，σ₂²），其中μ₁，μ₂，σ1²，σ2²都是未知的，S₁²是来自X的简单随机样本X₁，X₂，…，X_n的方差，S₂²是来自Y的简单随机样本Y₁，Y₂，…，Y_n的方差，则的置信度为1-α的置信区间为（ ）.

精解 在μ₁，μ₂未知时，的置信度为1-α的置信区间为

因此本题选A.

例8.5.3 设0.50，1.25，0.80，2.00是来自总体X的简单随机样本的观察值，已知Y=lnX服从正态分布N（μ，1）.

（1）求μ的置信度为0.95的置信区间；

（2）记b=EX，求b的置信度为0.90的置信区间.

精解 （1）在已知σ时，μ的置信度为0.95（即α=0.05）的置信区间为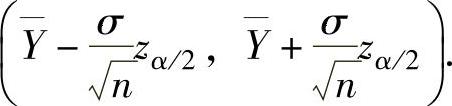

由于Y的样本值ln0.50，ln1.25，ln0.80，ln2.00的均值为

所以，μ的置信度为0.95的置信区间为

（2）由Y=lnX得X=e^Y，所以

由此可知，要计算b的置信度为0.90的置信区间，应先算出μ的置信度为0.90（此时α=0.10）的置信区间.

与（1）类似可得，μ的置信度为0.90的置信区间为

由于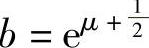是μ的单调增加函数，所以b的置信度为0.90的置信区间为

例8.5.4 设（X₁，X₂，…，X_n）和（Y₁，Y₂，…，Y_n）是分别来自总体X～N（μ₁，σ²），和Y～N（μ₂，σ²）的两个独立简单随机样本.求使μ₁-μ₂的置信度为0.90的置信区间长度等于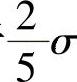（σ已知）的样本容量.

精解 σ²已知时，μ₁-μ₂的置信度为0.90（此时α=0.10）的置信区间的长度为 （其中z_α/2=z_0.05=1.645）.

于是，由题设得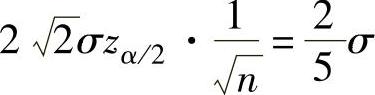，即

因此样本容量至少为136.