【主要内容】
1.傅里叶级数
设f(x)是以2l(l>0)为周期的周期函数,且在[-l,l]上可积,则称三角级数
为f(x)的以2l为周期的傅里叶级数,其中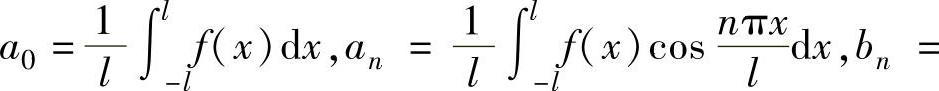
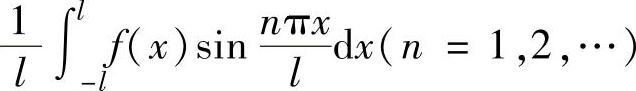 称为f(x)的傅里叶系数.
称为f(x)的傅里叶系数.
2.狄利克雷收敛定理
设f(x)是以2l为周期的周期函数,在[-l,l]上只有有限个第一类间断点和有限个极值点,则f(x)的傅里叶级数(∗)的收敛域为(-∞,+∞),和函数s(x)是以2l为周期的周期函数,其中在一个周期[-l,l]上有
以上称为狄利克雷收敛定理.
由狄利克雷收敛定理可以确定f(x)的傅里叶展开式
的成立范围.
注 (ⅰ)当f(x)是以2l为周期的偶函数时,f(x)以2l为周期的傅里叶级数为
当f(x)是以2l为周期的奇函数时,f(x)以2l为周期的傅里叶级数为
其中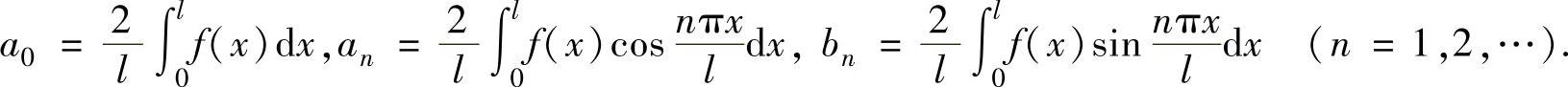
(ⅱ)当f(x)是以2π为周期的周期函数时,f(x)以2π为周期的傅里叶级数为
其中,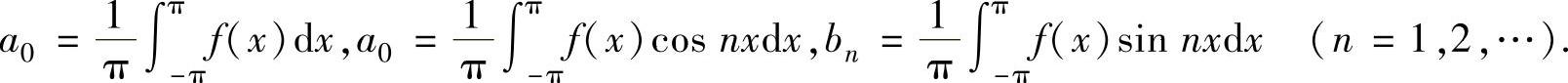
(ⅲ)仅在[-l,l]上定义的函数f(x),要展开成傅里叶级数,需将f(x)作以2l为周期的周期延拓,此时傅里叶展开式仍为式(∗∗),其成立范围是由狄利克雷收敛定理确定的范围与[-l,l]的交集.
仅在[0,l]上定义的函数f(x),要展开成傅里叶级数,需将f(x)作以l为周期的周期延拓,此时傅里叶展开式为
(其中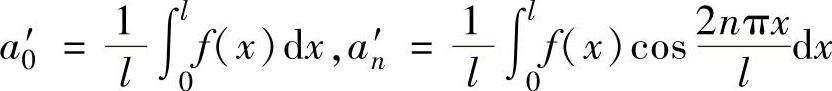 ,
,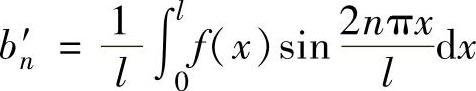 ,n=1,2,…),其成立范围是由狄利克雷收敛定理确定的范围与[0,l]的交集.
,n=1,2,…),其成立范围是由狄利克雷收敛定理确定的范围与[0,l]的交集.
仅在[0,l]上定义的函数f(x),要展开成余弦级数,需将f(x)作以2l为周期的偶延拓,此时余弦级数展开式为
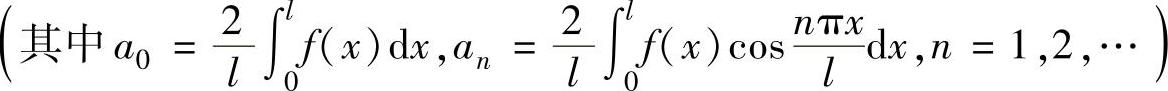 ,其成立范围是由狄利克雷收敛定理确定的范围与[0,l]的交集.
,其成立范围是由狄利克雷收敛定理确定的范围与[0,l]的交集.
仅在[0,l]上定义的函数f(x),要展开成正弦级数,需将它作以2l为周期的奇延拓,此时正弦级数展开式为
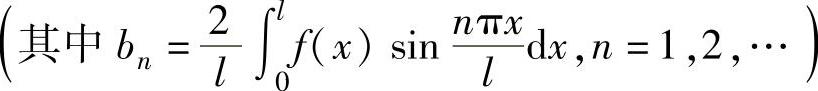 ,其成立的范围是由狄利克雷收敛定理确定的范围与[0,l]的交集.
,其成立的范围是由狄利克雷收敛定理确定的范围与[0,l]的交集.
【典型例题】(https://www.xing528.com)
例4.16.1 (单项选择题)设函数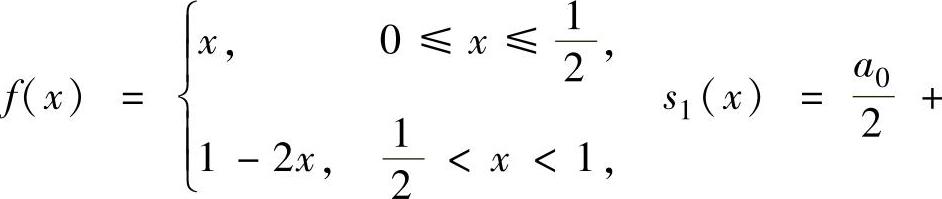
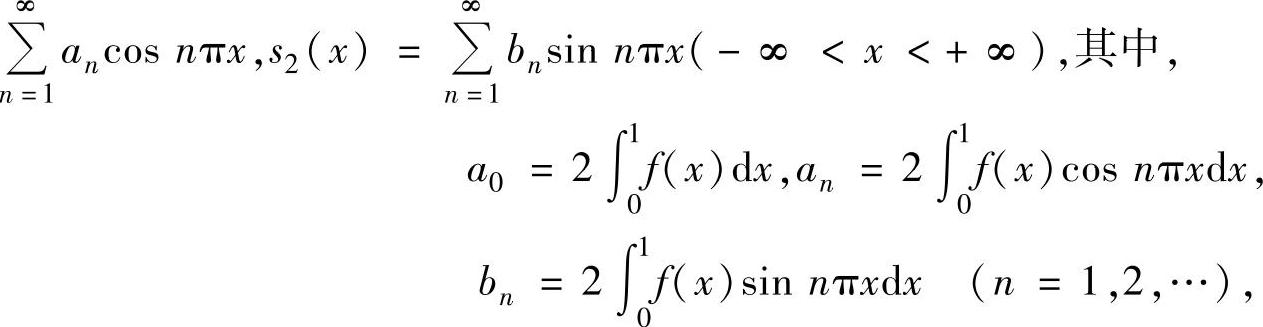 则
则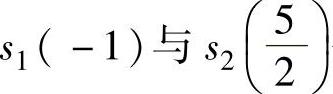 分别为( ).
分别为( ).
精解 s1(x),s2(x)分别是以2为周期的周期函数F1(x),F2(x)的傅里叶级数的和函数,其中
于是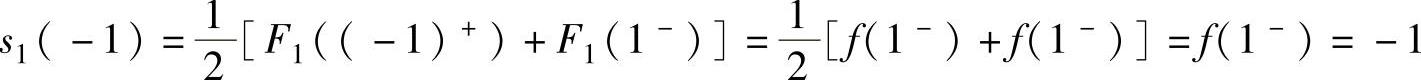 ,
,
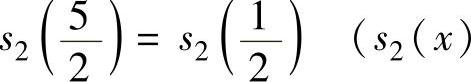 是以2为周期的周期函数)
是以2为周期的周期函数)
因此本题选B.
例4.16.2 设函数f(x)是以4为周期的周期函数,其中在[-2,2]上
求f(x)的以4为周期的傅里叶级数、和函数s(x)及傅里叶展开式.
精解 由于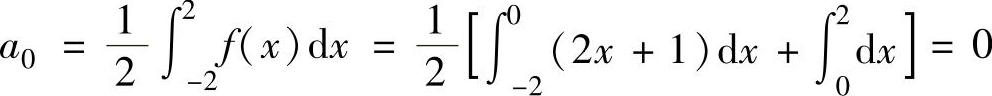 ,
,
n=1,2,…,所以f(x)的傅里叶级数为
由于f(x)在[-2,2]上满足狄利克雷收敛定理,所以式(1)的和函数s(x)是以4为周期的周期函数,其中在一个周期[-2,2]上的表达式为
由此可知,f(x)与s(x)仅在x=±2(2m+1)(m=0,1,2,…)处不等,因此有
例4.16.3 将函数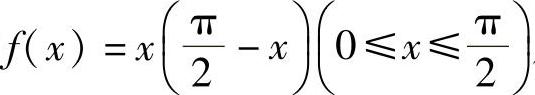 展开成余弦级数和正弦级数.
展开成余弦级数和正弦级数.
精解 由于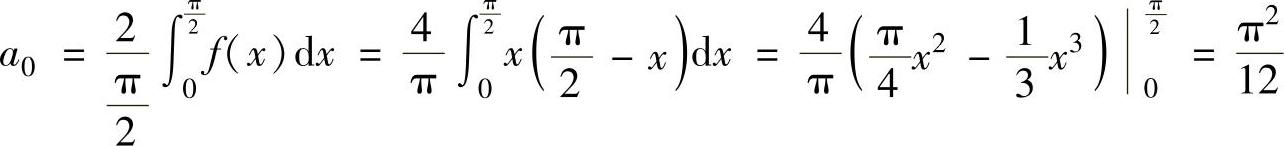 ,
,
n=1,2,…,所以
f(x)的余弦级数为
由于它是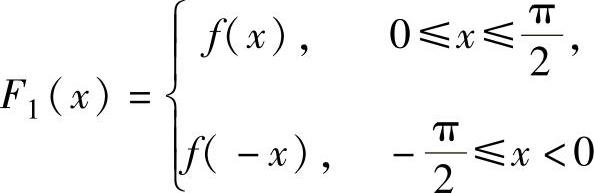 (即f(x)的偶延拓)的周期为π的傅里叶级数,所以由狄利克雷收敛定理知,式(1)的和函数
(即f(x)的偶延拓)的周期为π的傅里叶级数,所以由狄利克雷收敛定理知,式(1)的和函数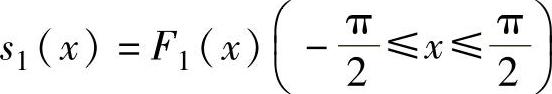 ,即
,即
从而有 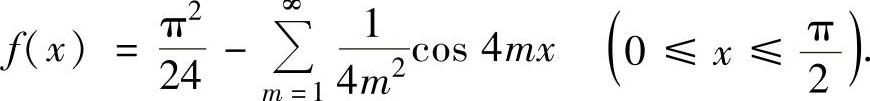
f(x)的正弦级数为
由于它是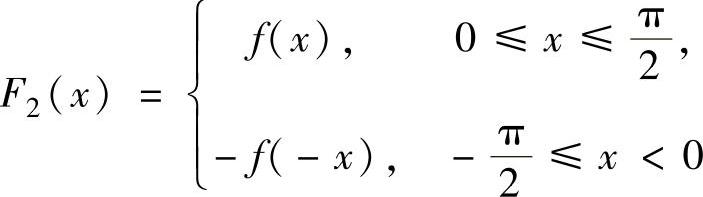 (即f(x)的奇延拓)的周期为π的傅里叶级数,所以由狄利克雷收敛定理知,式(2)的和函数
(即f(x)的奇延拓)的周期为π的傅里叶级数,所以由狄利克雷收敛定理知,式(2)的和函数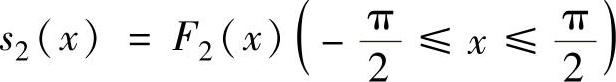 ,即
,即
从而有 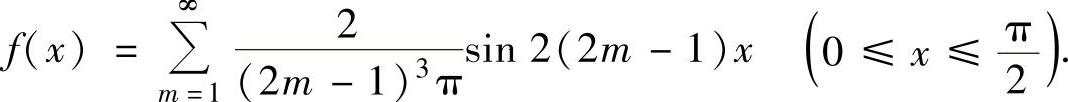
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




