【主要内容】
1.求幂级数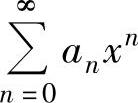 和函数的方法
和函数的方法
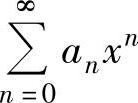 的和函数可按以下方法计算:
的和函数可按以下方法计算:
(1)对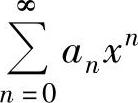 进行适当的代数运算(例如,将
进行适当的代数运算(例如,将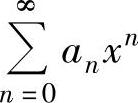 的各项同乘以一个常数或xk,或者提出一个常数或xk,k为某个正整数),或作适当的变量代换,使其成为常用函数的麦克劳林级数,从而求得
的各项同乘以一个常数或xk,或者提出一个常数或xk,k为某个正整数),或作适当的变量代换,使其成为常用函数的麦克劳林级数,从而求得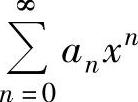 的和函数s(x).有时将
的和函数s(x).有时将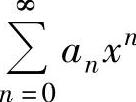 表示成几个幂级数之和,然后对每个幂级数都作以上处理,由此算得
表示成几个幂级数之和,然后对每个幂级数都作以上处理,由此算得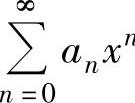 n的和函数s(x).
n的和函数s(x).
(2)对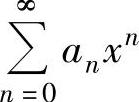 在收敛区间内进行求导或积分运算,使其成为某个常用函数的麦克劳林级数或几个常用函数的麦克劳林级数之和,由此求得
在收敛区间内进行求导或积分运算,使其成为某个常用函数的麦克劳林级数或几个常用函数的麦克劳林级数之和,由此求得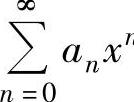 的和函数s(x).
的和函数s(x).
(3)当利用方法(1)或方法(2)不易求得幂级数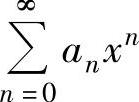 的和函数s(x)时,可通过对
的和函数s(x)时,可通过对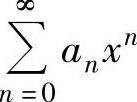 求导,建立它的和函数s(x)应满足的微分方程,然后解此微分方程得到s(x).
求导,建立它的和函数s(x)应满足的微分方程,然后解此微分方程得到s(x).
2.求幂级数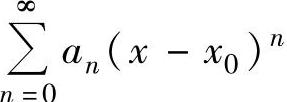 和函数的方法
和函数的方法
令y=x-x0,所给幂级数成为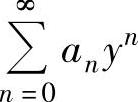 ,利用上一段所述方法算出它的和函数,记为s1(y),则
,利用上一段所述方法算出它的和函数,记为s1(y),则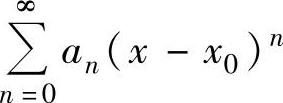 的和函数s(x)=s1(x-x0).
的和函数s(x)=s1(x-x0).
【典型例题】
例4.15.1 求幂级数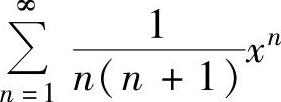 的和函数s(x).
的和函数s(x).
精解 所给幂级数的收敛域为[-1,1],对任意x∈[-1,1)有
其中,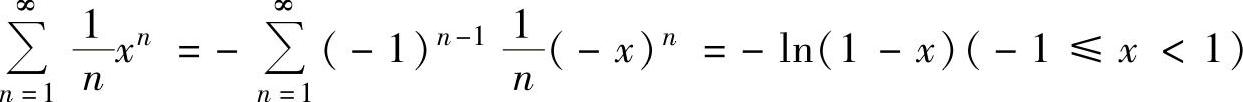 ,
,
将它们代入式(1)得
即 当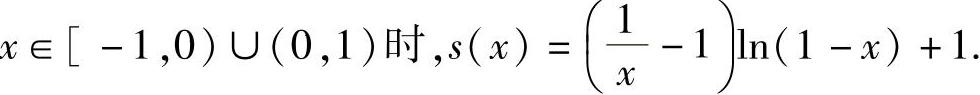
此外,
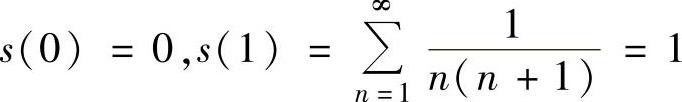 ,
,
综上所述,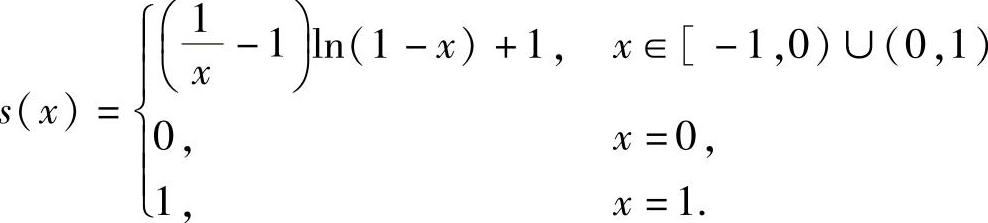 ,
,
例4.15.2 求幂级数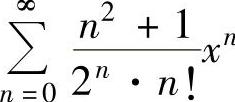 的收敛域与和函数s(x).
的收敛域与和函数s(x).
精解 由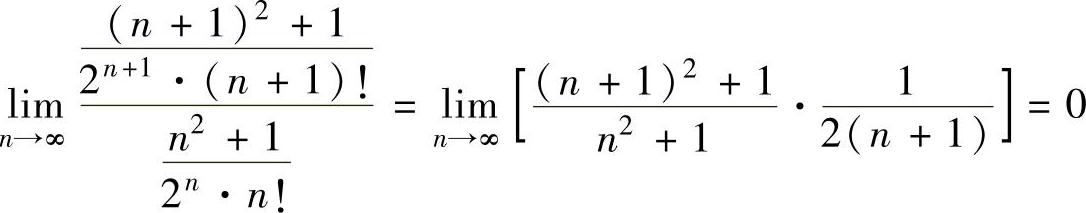 知,所给幂级数的收敛半径R=+∞,由此得收敛域为(-∞,+∞).对任意x∈(-∞,+∞)有
知,所给幂级数的收敛半径R=+∞,由此得收敛域为(-∞,+∞).对任意x∈(-∞,+∞)有
例4.15.3 求幂级数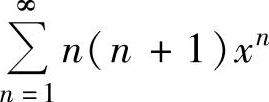 的和函数s(x).
的和函数s(x).
精解 记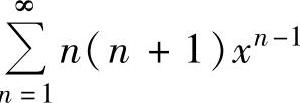 的和函数为s1(x),则
的和函数为s1(x),则
s(x)=xs1(x). (1)
由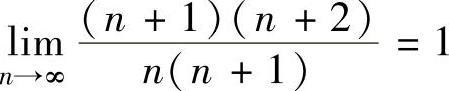 知
知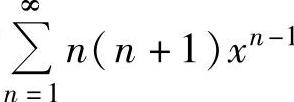 的收敛半径为R=1,收敛区间为(-1,1),并且x=-1,1都不是收敛点,所以收敛域为(-1,1),即
的收敛半径为R=1,收敛区间为(-1,1),并且x=-1,1都不是收敛点,所以收敛域为(-1,1),即
于是
式(2)的两边在(-1,1)内积分得
式(3)两边对x求二阶导数得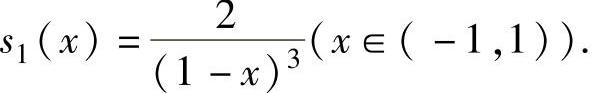
代入式(1)得 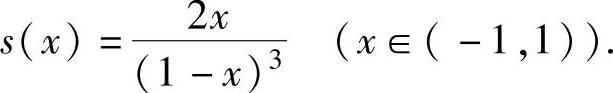
注 由以上三个例题可知,当幂级数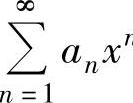 n的系数如
n的系数如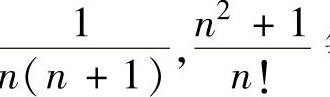 等是关于n的有理分式时,通常用逐项求导求和函数;当幂级数
等是关于n的有理分式时,通常用逐项求导求和函数;当幂级数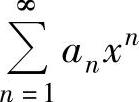 的系数如n(n+1)等是关于n的整式时,通常用逐项积分求和函数.(https://www.xing528.com)
的系数如n(n+1)等是关于n的整式时,通常用逐项积分求和函数.(https://www.xing528.com)
例4.15.4 求幂级数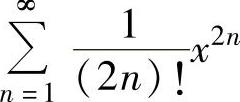 的收敛域与和函数s(x).
的收敛域与和函数s(x).
精解 由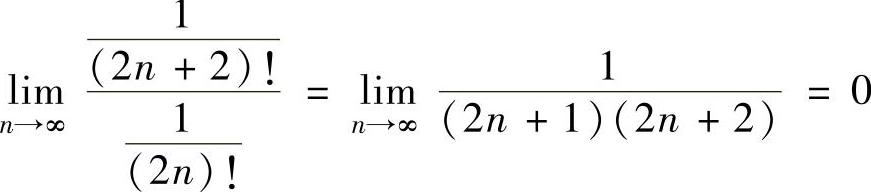 知,所给幂级数的收敛半径为+∞,从而收敛域为(-∞,+∞).对任意x∈(-∞,+∞),
知,所给幂级数的收敛半径为+∞,从而收敛域为(-∞,+∞).对任意x∈(-∞,+∞),
在式(1)的两边分别求两次导数得
比较式(1)、式(3)得
s″(x)-s(x)=1 (二阶常系数非齐次线性微分方程). (4)
式(4)对应的齐次线性微分方程为
s″(x)-s(x)=0, (5)
它的特征方程r2-1=0的根为r=-1,1,所以式(5)的通解为
s(x)=C1e-x+C2ex.
此外,式(4)有特解s(x)=-1.所以式(4)的通解为
s(x)=C1e-x+C2ex-1, (6)
以及 s′(x)=-C1e-x+C2ex. (7)
由式(1)、式(2)得s(0)=s′(0)=0.将它们分别代入式(6)、式(7)得
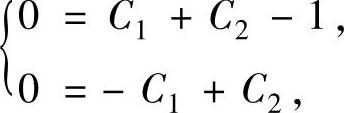 即
即 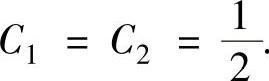
将它们代入式(6)得所求的和函数为
注 本题也可以按以下方法求解:
例4.15.5 求幂级数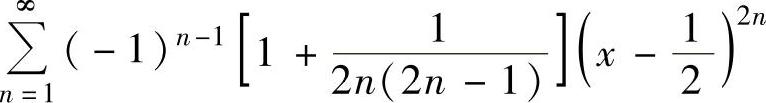 的收敛域与和函数s(x).
的收敛域与和函数s(x).
精解 显然,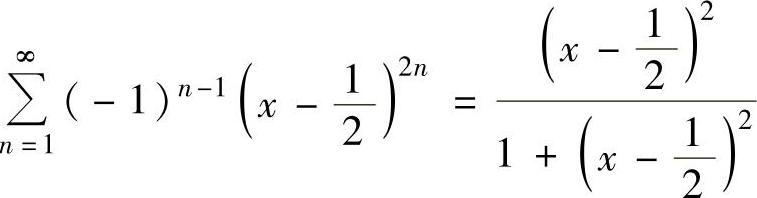 ,它的成立范围为
,它的成立范围为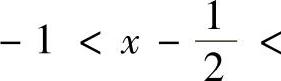 1,即
1,即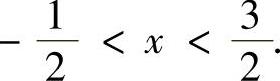
下面计算
的收敛域与和函数s1(x).
由于式(1)是缺项幂级数,所以利用正项级数比较判别法计算它的收敛域:
由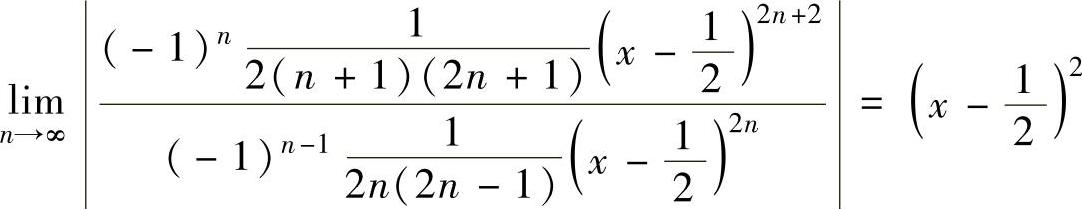 知,在
知,在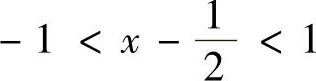 ,即
,即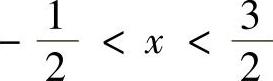 时,
时,
成立,因此,题中所给幂级数的收敛域为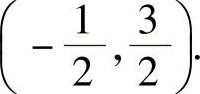
在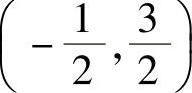 内,式(2)两边对x分别求两次导数得
内,式(2)两边对x分别求两次导数得
对于任意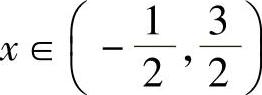 ,式(3)积分得
,式(3)积分得
对于任意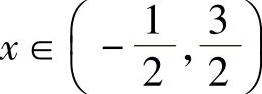 ,式(4)积分得
,式(4)积分得
综上所述,对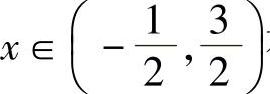 有
有
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




