【主要内容】
1.函数展开成幂级数的概念
设函数f(x)在点x0的某个邻域内有定义.如果存在幂级数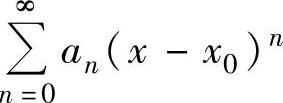 ,使得这个邻域内的任意x都有
,使得这个邻域内的任意x都有
则称f(x)在点x0处能展开成幂级数,或称f(x)在点x0的这个邻域内能展开成关于x-x0的幂级数.
如果f(x)在点x0的某个邻域内具有任意阶导数,则称幂级数
为f(x)在点x0处的泰勒级数.特别地,称f(x)在点x=0处的泰勒级数
为f(x)的麦克劳林级数.
如果f(x)在点x0能展开成幂级数,则这个幂级数必为f(x)在点x0处的泰勒级数,此时对点x0的某个邻域内的任意x有
称这一表达式为f(x)在点x0处的泰勒展开式.特别地,称f(x)在点x=0处的泰勒展开式
为f(x)的麦克劳林展开式.
2.函数能展开成泰勒级数的充分必要条件
设函数f(x)在点x0的某个邻域内具有任意阶导数,则f(x)在点x0处能展开成泰勒级数,即在点x0的某个邻域内有
的充分必要条件是对上述邻域内的任意x都有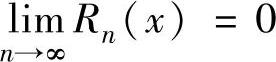 ,其中
,其中
(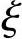 n是介于x0与x之间的实数,且与n有关),即f(x)在点x0处的n阶泰勒公式的拉格朗日型余项.
n是介于x0与x之间的实数,且与n有关),即f(x)在点x0处的n阶泰勒公式的拉格朗日型余项.
3.常用函数的麦克劳林展开式
时,展开式的成立范围分别为-1<x<1,-1<x≤1,-1≤x≤1),特别地,
4.函数展开成幂级数的方法
通常采用间接法,将函数展开成幂级数.
(1)将f(x)展开成关于x的幂级数
要将f(x)展开成关于x的幂级数,可以将f(x)表示成常用函数ex,sinx,cosx,ln(1+x),(1+x)α或它们的线性组合(注意:这里的线性组合中的系数可以是常数,也可以是x的正整数次幂),或通过变量代换与对f(x)进行求导、积分等运算使它成为常用函数ex,sinx,cosx,ln(1+x),(1+x)α或它们的线性组合,然后利用常用函数的麦克劳林展开式以及幂级数在收敛区间内的基本性质,将f(x)展开成关于x的幂级数.
(2)将f(x)展开成关于x-x0的幂级数
令t=x-x0,记φ(t)=f(t+x0),将φ(t)按(1)中所述方法展开成关于t的幂级数,
于是f(x)的幂级数展开式为
注 幂级数在收敛区间内的基本性质:
设幂级数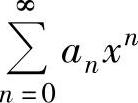 的收敛半径为R,其和函数为s(x),即
的收敛半径为R,其和函数为s(x),即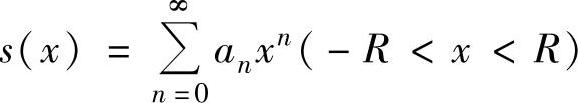 ,则
,则
(ⅰ)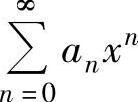 在收敛区间内绝对收敛,s(x)在收敛域上连续,在收敛区间内可导.
在收敛区间内绝对收敛,s(x)在收敛域上连续,在收敛区间内可导.
(ⅱ)对x∈(-R,R)有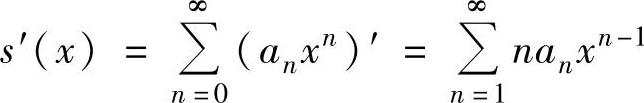 (即在收敛区间内,幂级数可逐项求导),
(即在收敛区间内,幂级数可逐项求导),
上式右边的幂级数的收敛半径仍为R,但它的收敛域与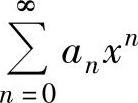 的收敛域未必相同,即当x=R是
的收敛域未必相同,即当x=R是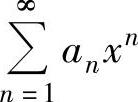 的收敛点时,未必也是
的收敛点时,未必也是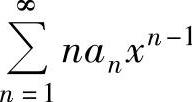 的收敛点,需具体检验;对点x=-R也有同样的说法.
的收敛点,需具体检验;对点x=-R也有同样的说法.
(ⅲ)对x∈(-R,R)有
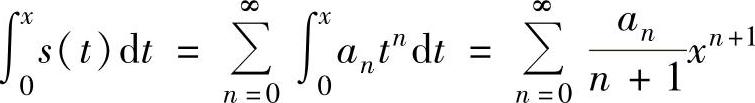 (即在收敛区间内,幂级数可逐项积分).
(即在收敛区间内,幂级数可逐项积分).
上式左边的幂级数的收敛半径仍为R,但它的收敛域与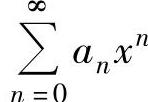 的收敛域未必相同,即当x=R不是
的收敛域未必相同,即当x=R不是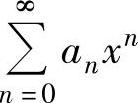 的收敛点时,也可能是
的收敛点时,也可能是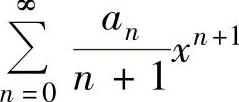 的收敛点,需具体检验;对点x=-R也有同样的说法.(https://www.xing528.com)
的收敛点,需具体检验;对点x=-R也有同样的说法.(https://www.xing528.com)
【典型例题】
例4.14.1 将下列函数展开成关于x的幂级数:
精解 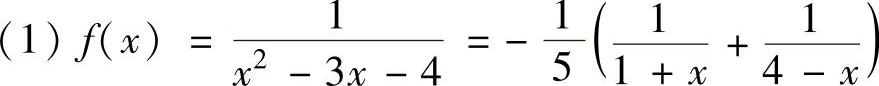
由于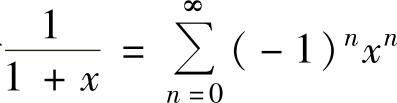 的成立范围为
的成立范围为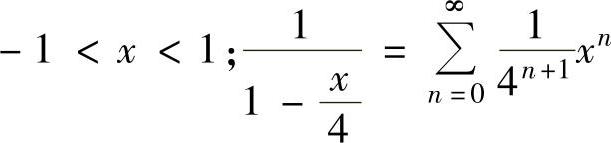 的成立范围为-4<x<4,所以式(1)的成立范围为-1<x<1.
的成立范围为-4<x<4,所以式(1)的成立范围为-1<x<1.
其中 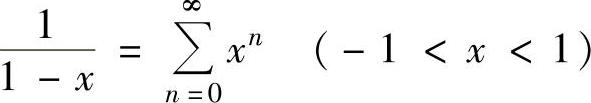 ,
,
将它们代入式(2)得
例4.14.2 将下列函数展开成关于x的幂级数:
(1)f(x)=ln(e-x);
(2)f(x)=cos2x.
精解 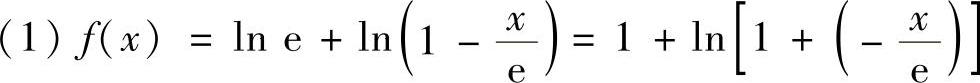
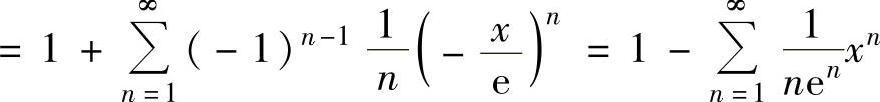 ,
,
上式成立的范围为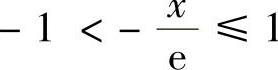 ,即-e≤x<e.
,即-e≤x<e.
(2)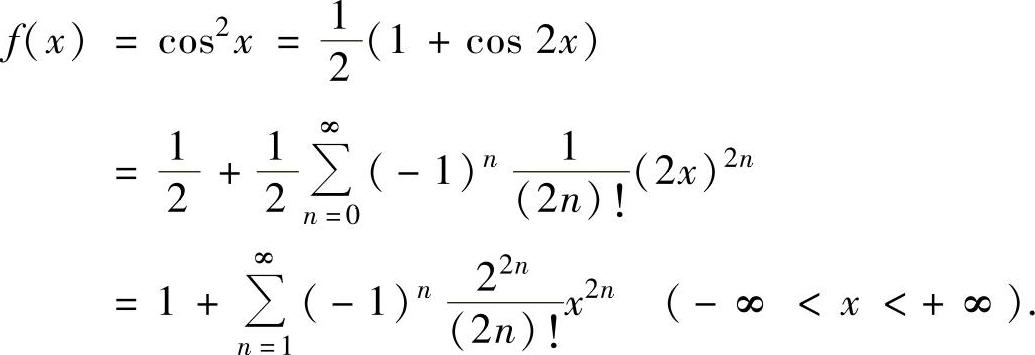
例4.14.3 将下列函数在点x=1处展开成幂级数:
(1)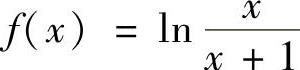 ;
;
(2)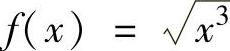 .
.
精解 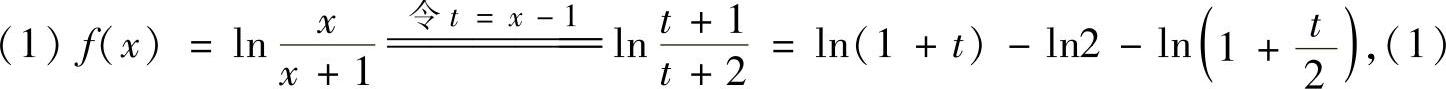
其中 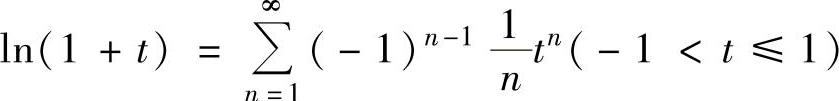 ,
,
将它们代入式(1)得
(2)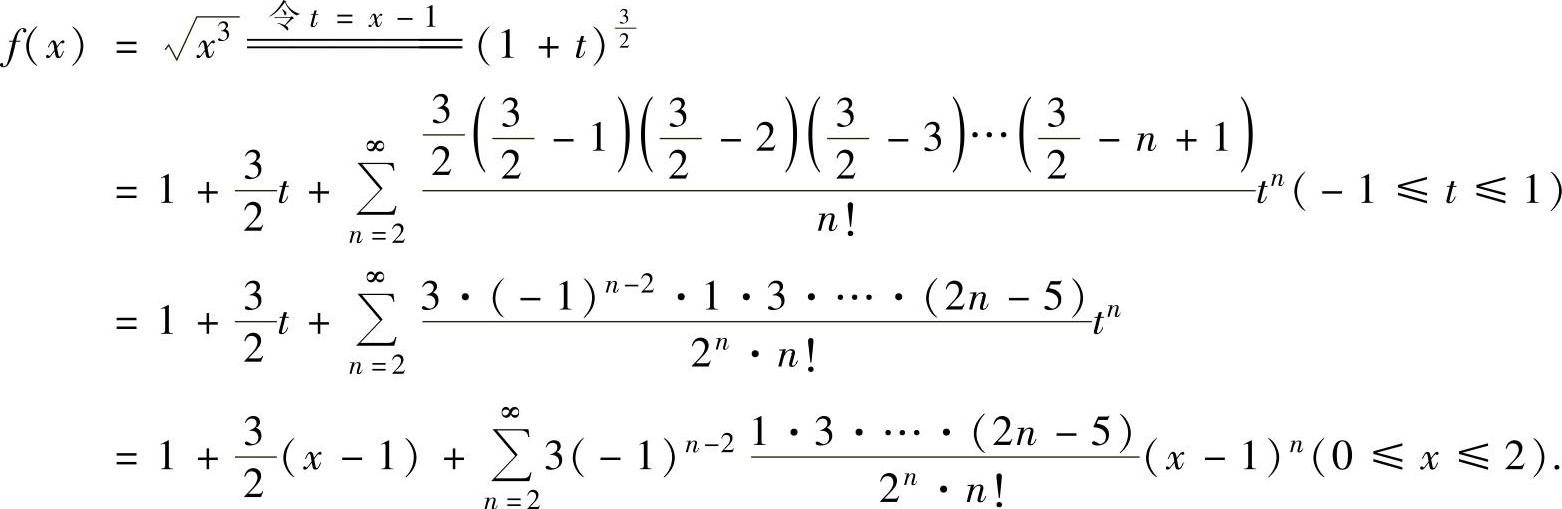
例4.14.4 将下列函数展开成关于x的幂级数:
(1)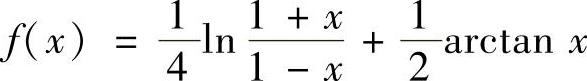 ;
;
(2)
精解 (1)f(x)不是常用函数的线性组合,所以从考虑f′(x)入手将f(x)展开成关于x的幂级数.
所以,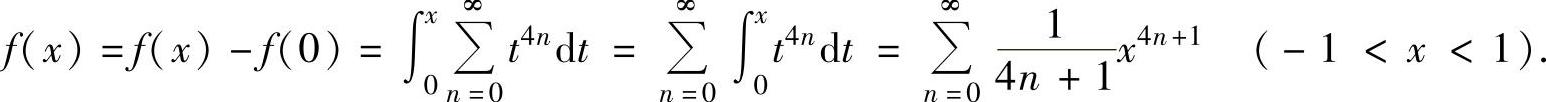
(2)由 知,只要将arctanx展开成x的幂级数即可得到f(x)的幂级数展开式.
知,只要将arctanx展开成x的幂级数即可得到f(x)的幂级数展开式.
所以 
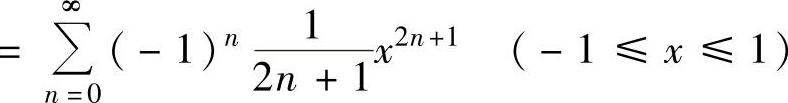 ,
,
将它们代入式(1)得
其中 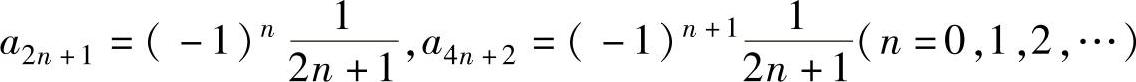 ,其他an=0.
,其他an=0.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




