【主要内容】
1.绝对收敛与条件收敛的概念
设级数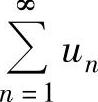 有无穷多个正项,也有无穷多个负项,则称
有无穷多个正项,也有无穷多个负项,则称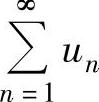 是任意项级数.
是任意项级数.
任意项级数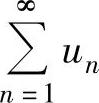 的收敛性分绝对收敛、条件收敛及发散.
的收敛性分绝对收敛、条件收敛及发散.
如果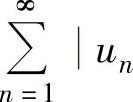 收敛,则称
收敛,则称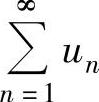 绝对收敛;如果
绝对收敛;如果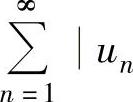 发散,但
发散,但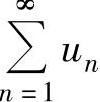 收敛,则称
收敛,则称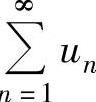 条件收敛.
条件收敛.
注(ⅰ)一般地,当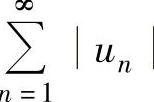 发散时,
发散时,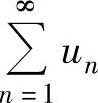 未必发散.但是,如果由正项级数比值判别法或根值判别法判定
未必发散.但是,如果由正项级数比值判别法或根值判别法判定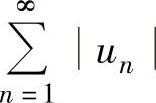 发散时,则
发散时,则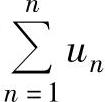 必发散.
必发散.
(ⅱ)如果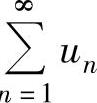 绝对收敛,则
绝对收敛,则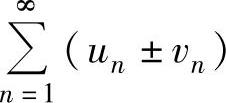 的收敛性与
的收敛性与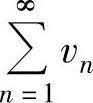 的收敛性相同.如果
的收敛性相同.如果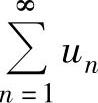 收敛(绝对收敛或条件收敛),
收敛(绝对收敛或条件收敛),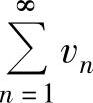 发散,则
发散,则 发散.
发散.
2.交错级数的莱布尼茨定理
设an>0(n=1,2,…),则称级数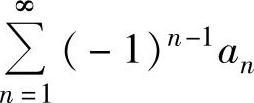 为交错级数,它是一种特殊的任意项级数.莱布尼茨定理:设正项数列{an}单调减少收敛于零,则交错级数
为交错级数,它是一种特殊的任意项级数.莱布尼茨定理:设正项数列{an}单调减少收敛于零,则交错级数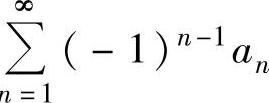 收敛.
收敛.
注 交错级数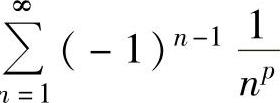 ,当p>1时,绝对收敛;当0<p≤1时,条件收敛;当p≤0时,发散.
,当p>1时,绝对收敛;当0<p≤1时,条件收敛;当p≤0时,发散.
【典型例题】
例4.12.1 (单项选择题)设正项级数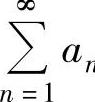 收敛,则对于常数
收敛,则对于常数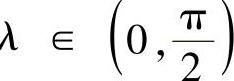 ,级数
,级数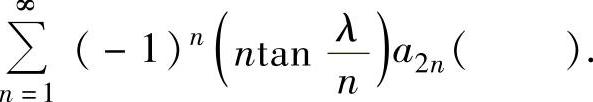
A.绝对收敛 B.条件收敛
C.发散 D.收敛性与λ有关
精解 由于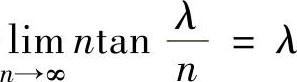 ,所以存在正数M,使得
,所以存在正数M,使得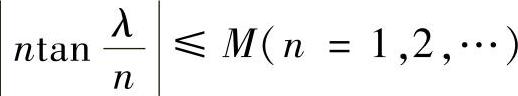 ,因此
,因此
此外,由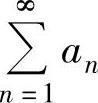 收敛知
收敛知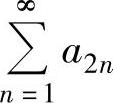 收敛.由此得到
收敛.由此得到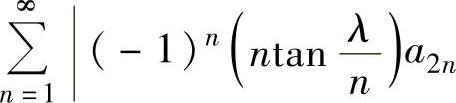 收敛,从而
收敛,从而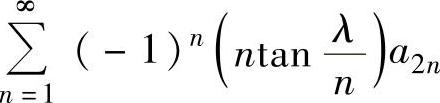 绝对收敛.
绝对收敛.
因此本题选A.
例4.12.2 (单项选择题)设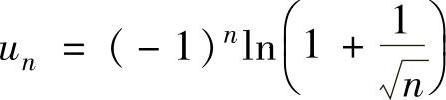 ,则级数( ).
,则级数( ).
A.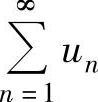 与
与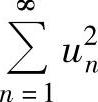 都收敛
都收敛
B.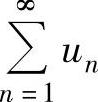 与
与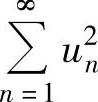 都发散
都发散
C.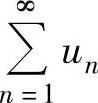 收敛而
收敛而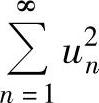 发散
发散
D.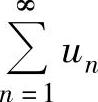 发散而
发散而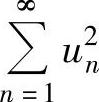 收敛
收敛
精解 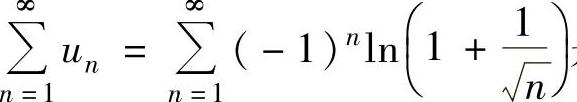 是交错级数,记
是交错级数,记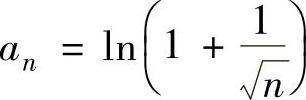 ,则{an}单调减少收敛于零,所以由交错级数的莱布尼茨定理知
,则{an}单调减少收敛于零,所以由交错级数的莱布尼茨定理知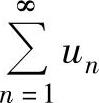 收敛.
收敛.
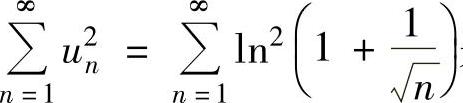 是正项级数.由于(https://www.xing528.com)
是正项级数.由于(https://www.xing528.com)
而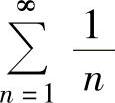 发散,所以
发散,所以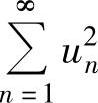 发散.
发散.
因此本题选C.
例4.12.3 判别级数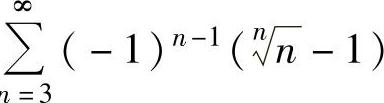 的收敛性.如果是收敛的,需指明其是绝对收敛的还是条件收敛的.
的收敛性.如果是收敛的,需指明其是绝对收敛的还是条件收敛的.
精解 记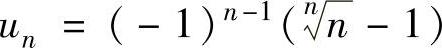 ,先考虑
,先考虑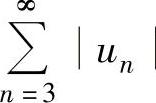 的收敛性.
的收敛性.
由于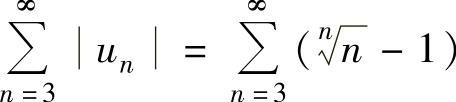 ,其中
,其中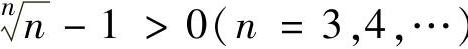 且
且
所以由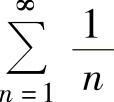 发散知
发散知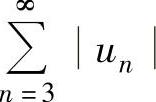 发散.
发散.
下面考虑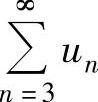 的收敛性.
的收敛性.
由于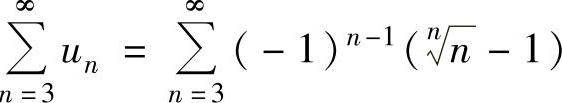 是交错级数,且
是交错级数,且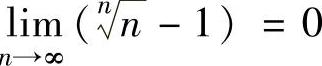 ,此外数列u3,u4,…单调减少(这是因为将n看做x,则由
,此外数列u3,u4,…单调减少(这是因为将n看做x,则由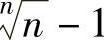 得函数
得函数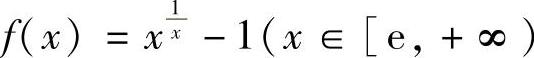 ,于是由
,于是由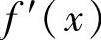
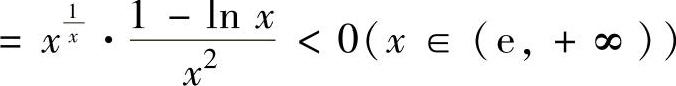 知f(x)在[e,+∞)上单调减少,从而u3,u4,…单调减少),所以由交错级数的莱布尼茨定理知
知f(x)在[e,+∞)上单调减少,从而u3,u4,…单调减少),所以由交错级数的莱布尼茨定理知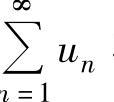 收敛.
收敛.
综上所述,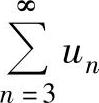 条件收敛.
条件收敛.
例4.12.4 设函数f(x)在[-1,1]上定义,在点x=0处二阶可导,且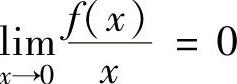 .证明:级数
.证明:级数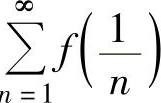 绝对收敛.
绝对收敛.
精解 只要证明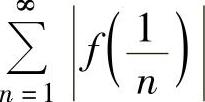 收敛即可.为此考虑函数f(x)在点x=0的某个邻域内的性态.
收敛即可.为此考虑函数f(x)在点x=0的某个邻域内的性态.
由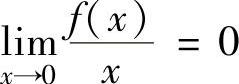 知,f(0)=0,f′(0)=0,此外,
知,f(0)=0,f′(0)=0,此外,
所以在点x=0的某个邻域(-δ,δ)(δ是某个正数)内有
f(x)≤Mx2(M是某个正数).
由此可知存在正整数N,当n>N时,有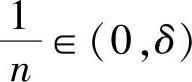 及
及
于是,由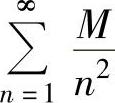 收敛得证
收敛得证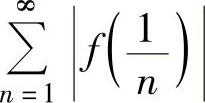 收敛,从而
收敛,从而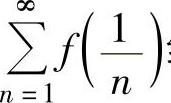 绝对收敛.
绝对收敛.
例4.12.5 判别级数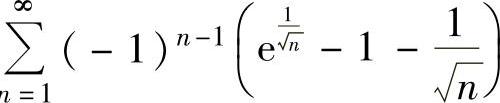 的收敛性.
的收敛性.
精解 记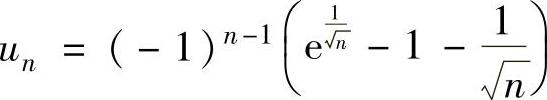 ,将
,将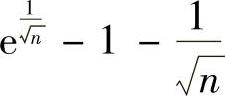 中的
中的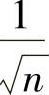 看做x得函数
看做x得函数
于是,当n充分大时有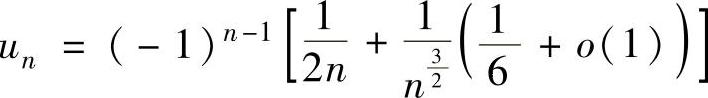
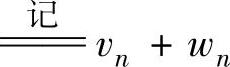 ,
,
由于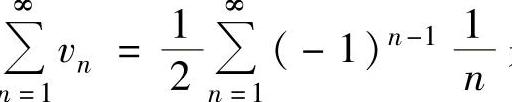 是p=1的级数
是p=1的级数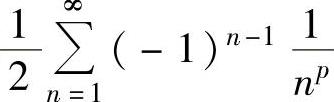 ,所以条件收敛,此外
,所以条件收敛,此外
而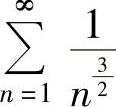 收敛,所以
收敛,所以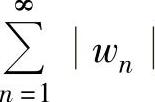 收敛,即
收敛,即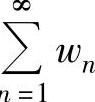 绝对收敛.因此
绝对收敛.因此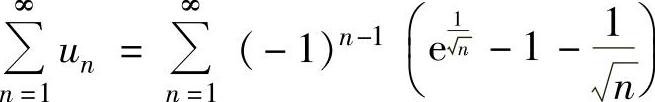 条件收敛.
条件收敛.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




