【摘要】:)上应用拉格朗日中值定理得,即有,并且即发散,所以由比较判别法知发散.
【主要内容】
1.比较判别法
设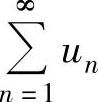 是正项级数,并可以找到正项级数
是正项级数,并可以找到正项级数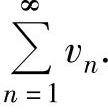
如果un≤vn(n=1,2,…),且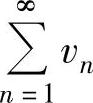 收敛,则
收敛,则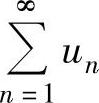 收敛.
收敛.
如果un≥vn(n=1,2,…),且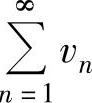 发散,则
发散,则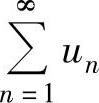 发散.
发散.
2.比较判别法的极限形式
设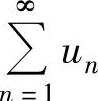 是正项级数,并可以找到正项级数
是正项级数,并可以找到正项级数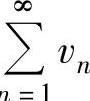 ,且
,且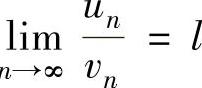 ;
;
如果0<l<+∞,则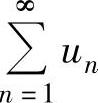 与
与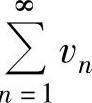 有相同的收敛性;
有相同的收敛性;
如果l=0,则由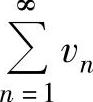 收敛可得
收敛可得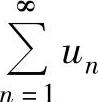 收敛;
收敛;
如果l=+∞,则由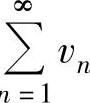 发散可得
发散可得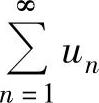 发散.
发散.
【典型例题】
例4.11.1 (单项选择题)设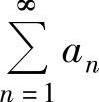 是正项级数,则下列结论正确的是( ).
是正项级数,则下列结论正确的是( ).
A.若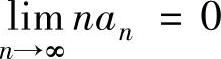 ,则
,则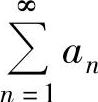 收敛
收敛
B.若存在非零常数λ,使得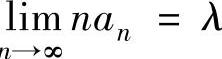 ,则
,则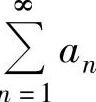 发散
发散
C.若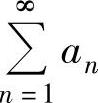 收敛,则
收敛,则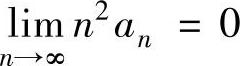
D.若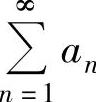 发散,则存在非零常数λ,使得
发散,则存在非零常数λ,使得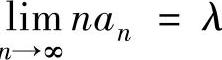
精解 顺序考虑各个选项,直到得到正确选项为止.
先考虑选项A.对正项级数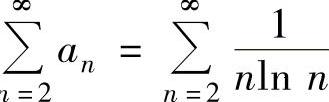 ,虽然
,虽然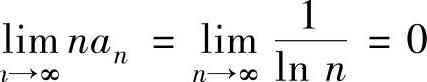 ,但
,但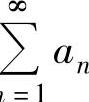 发散(https://www.xing528.com)
发散(https://www.xing528.com)
(详见本节例4.11.4),所以选项A不能选.
再考虑选项B.由于
而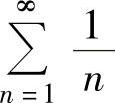 发散,所以由比较判别法的极限形式知
发散,所以由比较判别法的极限形式知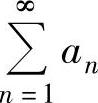 发散,即选项B正确.
发散,即选项B正确.
因此本题选B.
例4.11.2 讨论正项级数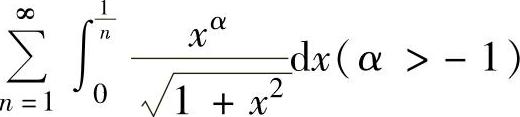 的收敛性.
的收敛性.
精解 用比较判别法讨论所给级数的收敛性.
记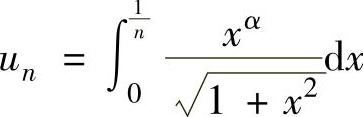 ,则
,则
因此,当α>0时,由正项级数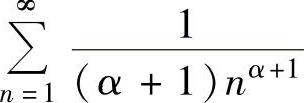 收敛知所给级数收敛;当-1<α≤0时,由正项级数
收敛知所给级数收敛;当-1<α≤0时,由正项级数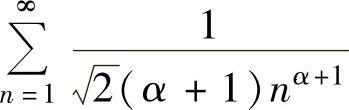 发散知所给级数发散.
发散知所给级数发散.
例4.11.3 判别级数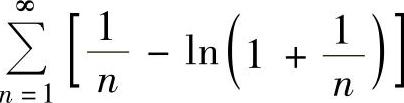 的收敛性.
的收敛性.
精解 由ln(1+x)<x(x>0)知所给级数是正项级数.下面用比较判别法的极限形式考虑它的收敛性.为此计算极限
将上式中的 看做x,则由
看做x,则由
得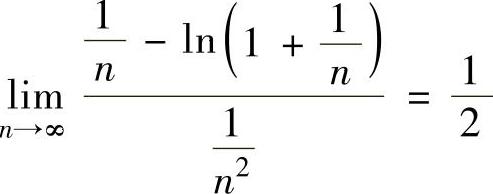 ,而
,而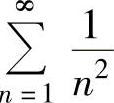 收敛,所以
收敛,所以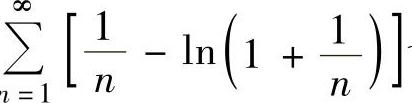 也收敛.
也收敛.
例4.11.4 证明正项级数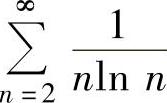 发散.
发散.
精解 记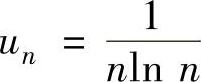 ,将它适当缩小,寻找一个发散的正项级数
,将它适当缩小,寻找一个发散的正项级数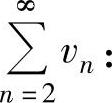 对lnlnx在[n,n+1](n=2,3,…)上应用拉格朗日中值定理得
对lnlnx在[n,n+1](n=2,3,…)上应用拉格朗日中值定理得
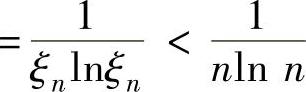 ,
,
即有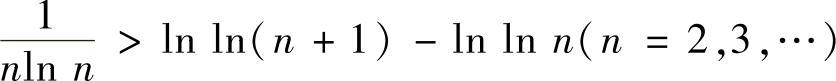 ,并且
,并且
即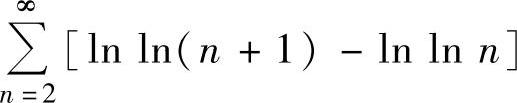 发散,所以由比较判别法知
发散,所以由比较判别法知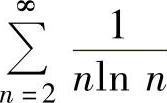 发散.
发散.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




