五、二阶常系数齐次线性微分方程

【主要内容】

1.二阶齐次线性微分方程解的构造

形如 y″+P（x）y′+Q（x）y=0（其中，P（x），Q（x）都是已知函数）（∗）的微分方程，称为二阶齐次线性微分方程.

如果y₁（x），y₂（x）是式（∗）的两个线性无关的特解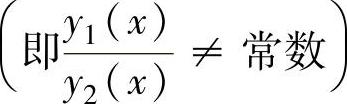，则

y=C₁y₁（x）+C₂y₂（x）

是式（∗）的通解.

2.二阶常系数齐次线性微分方程的通解

形如

y″+py′+qy=0 （其中，p，q都是常数） （∗∗）

的微分方程，称为二阶常系数齐次线性微分方程.

称r²+pr+q=0为式（∗∗）的特征方程.

关于（∗∗）的通解有以下结论：

（1）如果特征方程有两个不等的实根r₁，r₂，则式（∗∗）的通解为

（2）如果特征方程有两个相等的实根r₁，r₂（r₁=r₂），则式（∗∗）的通解为

（3）如果特征方程有一对共轭复根r_1，2=α±iβ（β≠0），则式（∗∗）的通解为

y（x）=e^αx（C₁cosβx+C₂sinβx）.

注 对于n阶常系数齐次线性微分方程

y^（n）+p₁y^（n-1）+p₂y^（n-2）+…+p_n-1y′+p_ny=0

的通解也有类似的结论.例如，对于四阶常系数齐次线性微分方程

y^（4）+p₁y‴+p₂y″+p₃y′+p₄y=0 （∗∗∗）

的特征方程r⁴+p₁r³+p₂r²+p₃r+p₄=0，如有4个互不相同的实根r₁，r₂，r₃，r₄时，式（∗∗∗）的通解为

如有实根r₁（二重）和r₂（二重）时，式（∗∗∗）的通解为

如有不同实根r₁，r₂及一对共轭复根α±iβ（β≠0）时，式（∗∗∗）的通解为

如有二重共轭复根α±iβ（β≠0）时，式（∗∗∗）的通解为

y（x）=e^αx[（C₁+C₂x）cosβx+（C₃+C₄x）sinβx].

【典型例题】

例4.5.1 设y=（C₁+C₂x）e^-2x+e^x（C₃cosx+C₄sinx）为某个常系数齐次线性微分方程的通解，试写出该微分方程.

精解 所求的微分方程应是四阶的，它的特征根为-2（二重）以及一对共轭复根1±i，所以特征方程为

（r+2）²（r-1-i）（r-1+i）=0，

即 （r²+4r+4）[（r-1）²+1]=0.化简整理后成为r⁴+2r³-2r²+8=0.所以所求的四阶常系数齐次线性微分方程为

y^（4）+2y‴-2y″+8=0.

例4.5.2 （单项选择题）设二阶常系数齐次线性微分方程

y″+ay′+by=0

的每个解y（x）都满足

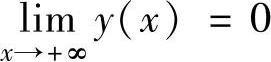，则a，b的取值范围为（ ）.

A.a>0，b<0 B.a<0，b<0

C.a>0，b>0 D.a<0，b>0(www.xing528.com)

精解 所给微分方程的特征方程为r²+ar+b=0.记它的两个特征根为r₁，r₂.由于每个解y（x）都满足

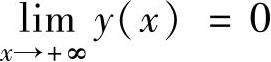，故r₁，r₂的实部都为负数，从而

a=-（r₁+r₂）>0， b=r₁·r₂>0，

因此本题选C.

例4.5.3 求微分方程

cosx·y″-2sinx·y′+3cosx·y=0

的通解.

精解 将所给微分方程改写成

（cosx·y″-2sinx·y′-cosx·y）+4cosx·y=0，

即 [cosx·y″+2（cosx）′y′+（cosx）″y]+4cosx·y=0. （1）

显然，式（1）左边方括号内为（cosx·y）″，所以式（1）为

（cosx·y）″+4cosx·y=0，

故令u=cosx·y，则所给微分方程成为

u″+4u=0 （二阶常系数齐次线性微分方程）.

它的特征方程r²+4=0的根为2i，-2i，所以通解为

u=C₁cos2x+C₂sin2x.

从而所给的微分方程通解为

cosx·y=C₁cos2x+C₂sin2x， 即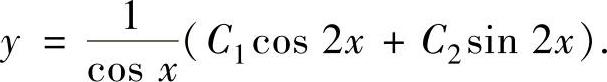

注 当所给的方程是齐次线性微分方程，但不是常系数时，可考虑作适当的变量代换，将所给的微分方程转换成常系数的.这是解稍复杂二阶线性微分方程常用的方法.

例4.5.4 设函数y=y（x）（x>0）满足微分方程

y″+y′-2y=0

及条件y（0）=6，y（ln2）=5.求函数φ（x）=y（lnx）的表达式.

精解 算出满足条件y（0）=6，y（ln2）=5的特解y=y（x），即可得到φ（x）的表达式.所给的微分方程是二阶常系数齐次线性微分方程，它的特征方程r²+r-2=0的根为r=-2，1.所以该微分方程的通解为

y=C₁e^-2x+C₂e^x. （1）

利用y（0）=6，y（ln2）=5得

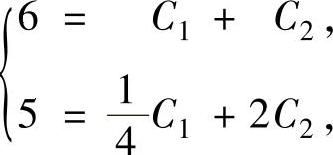即 C₁=4，C₂=2.

将它们代入式（1）得

y=4e^-2x+2e^x.

于是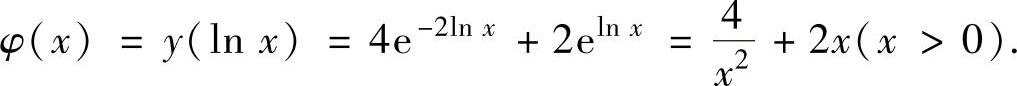

例4.5.5 求微分方程y″+2ky′+y=0（k是常数）的通解.

精解 所给微分方程是二阶常系数齐次线性微分方程，它的特征方程r²+2kr+1=0的根为

于是，当|k|>1时，r₁，r₂是两个不同的实数，此时所给微分方程的通解为

当|k|=1时，r₁=r₂=-k，此时所给微分方程的通解为

y=（C₁+C₂x）e^-kx；

当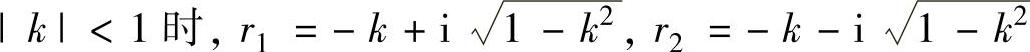是一对共轭复根，此时所给微分方程的通解为