【主要内容】
1.斯托克斯公式与旋度的概念
设三元函数P(x,y,z),Q(x,y,z),R(x,y,z)都具有连续偏导数,Γ是光滑或分段光滑空间有向闭曲线;Σ是以Γ为边界的任意光滑或分块光滑的曲面,其上任一点的法向量与Γ的方向符合右手法则,则有以下的斯托克斯公式:
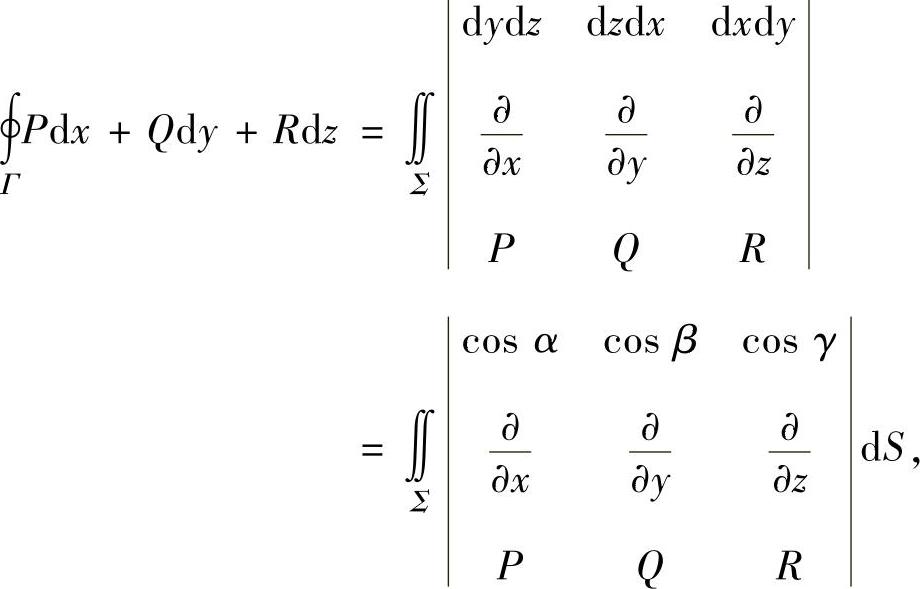
其中(cosα,cosβ,cosγ)是有向曲面Σ上任一点的单位法向量n0(n0dS=(cosαdS,cosβdS,cosγdS)=(dydz,dzdx,dxdy))
记向量场A(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k,则称
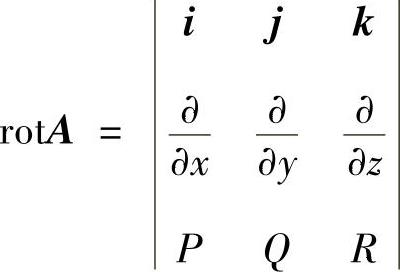
为A的旋度,于是斯托克斯公式也可以表示为
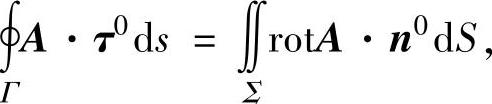
其中τ0是有向曲线Γ上任一点的单位切向量(τ0ds=(dx,dy,dz)).
2.斯托克斯公式应用的推广
应用斯托克斯公式计算曲线积分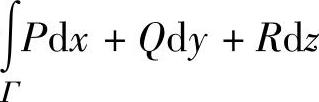 时,要求Γ是正向闭曲线.但当Γ不是闭曲线时,可以适当添加一段曲线(记为Γ1),使得Γ+Γ1为闭曲线,并且使
时,要求Γ是正向闭曲线.但当Γ不是闭曲线时,可以适当添加一段曲线(记为Γ1),使得Γ+Γ1为闭曲线,并且使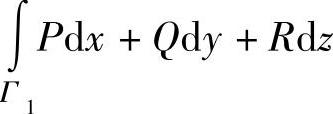 比
比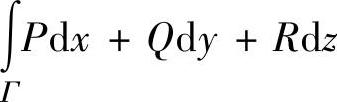 容易计算,于是对
容易计算,于是对
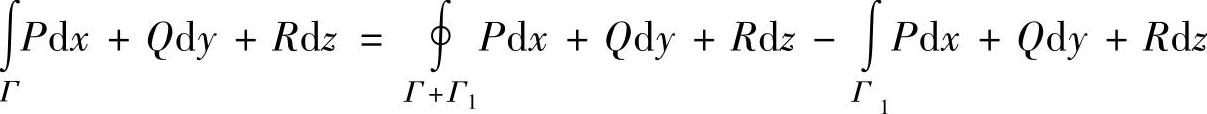
的右边第一项应用斯托克斯公式可较快地算出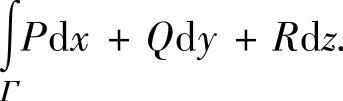
【典型例题】
例3.20.1 计算关于坐标的曲线积分
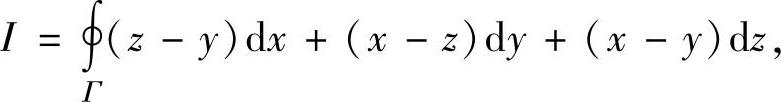
其中Γ是曲线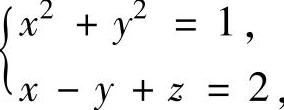 从z轴正向往z轴负向看过去,Γ是顺时针的.
从z轴正向往z轴负向看过去,Γ是顺时针的.
精解 由于Γ是闭曲线,所以可应用斯托克斯公式计算I.
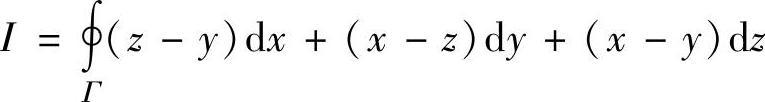
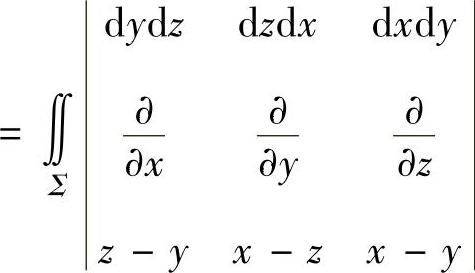 (其中Σ是平面x-y+z=2上由Γ围成的那一部分的下侧,Σ在xOy平面上的投影为Dxy={(x,y)|x2+y2≤1})
(其中Σ是平面x-y+z=2上由Γ围成的那一部分的下侧,Σ在xOy平面上的投影为Dxy={(x,y)|x2+y2≤1})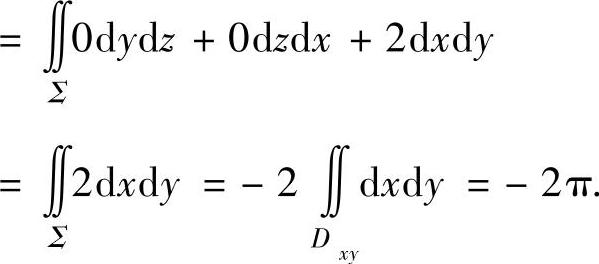
例3.20.2 计算关于坐标的曲线积分
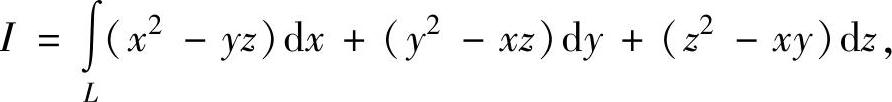
其中,L是圆柱面x2+y2=R2上的螺线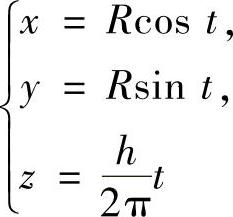 (其中R>0,h>0)从点A(R,0,0)到点B(R,0,h)的弧段.
(其中R>0,h>0)从点A(R,0,0)到点B(R,0,h)的弧段.
精解 虽然L不是闭曲线,但添加线段B ,构成闭曲线
,构成闭曲线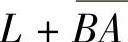 ,可间接应用斯托克斯公式计算I.
,可间接应用斯托克斯公式计算I.
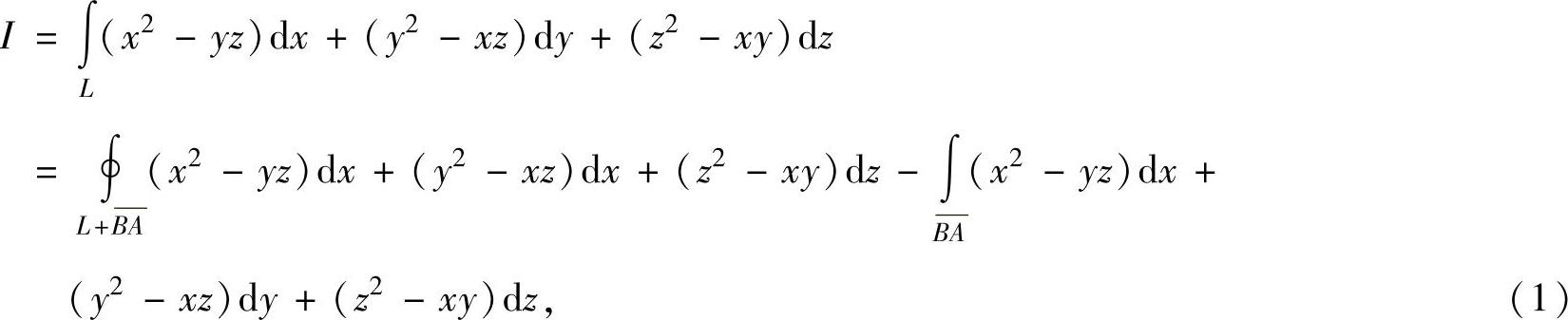 (https://www.xing528.com)
(https://www.xing528.com)
其中,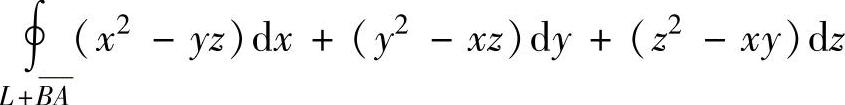
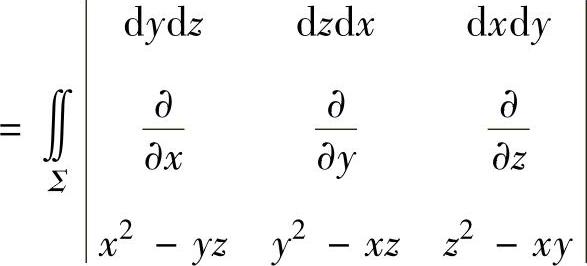 (其中Σ是柱面x2+y2=R2上的由L+BA围成的曲面的外侧)
(其中Σ是柱面x2+y2=R2上的由L+BA围成的曲面的外侧)

由于BA的参数方程为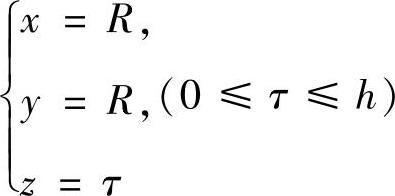 ,其中B,A分别对应参数τ=h,τ=0,所以,
,其中B,A分别对应参数τ=h,τ=0,所以,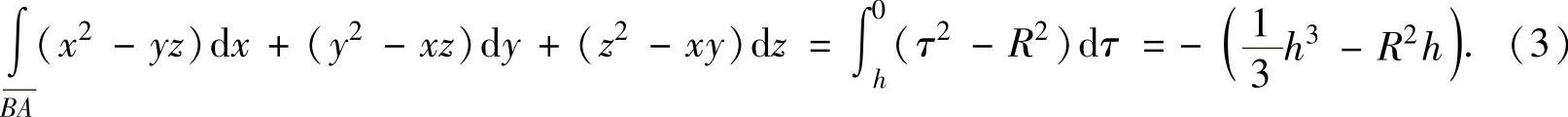
将式(2)、式(3)代入式(1)得

例3.20.3 计算关于坐标的曲线积分
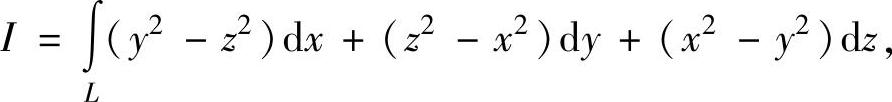
其中,L是球面x2+y2+z2=a2(a>0)在第一卦限中的有向边界曲线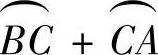 ,如图3.20.3所示.
,如图3.20.3所示.
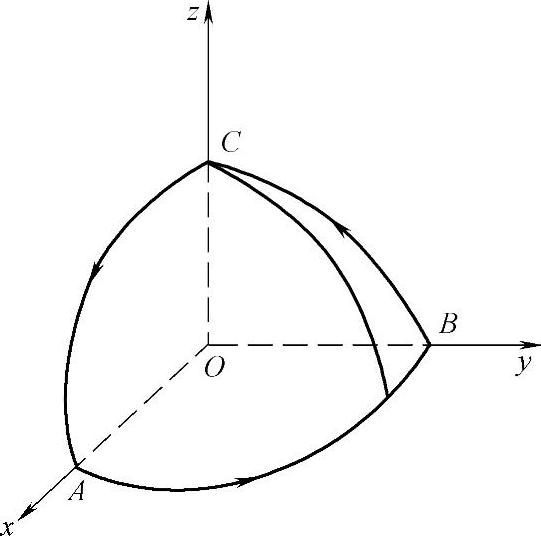
图 3.20.3
精解 L不是闭曲线,所以添上有向弧 (即球面x2+y2+z2=a2在第一卦限中的另一有向边界),使得
(即球面x2+y2+z2=a2在第一卦限中的另一有向边界),使得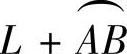 是闭曲线,然后考虑应用斯托克斯公式.
是闭曲线,然后考虑应用斯托克斯公式.
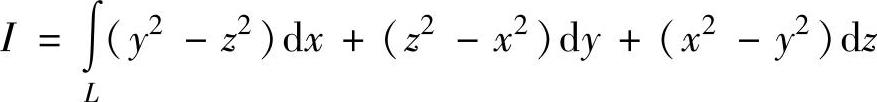
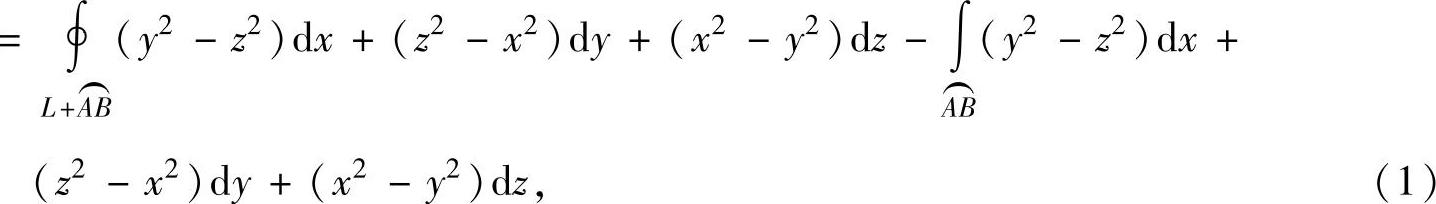
其中,
其中
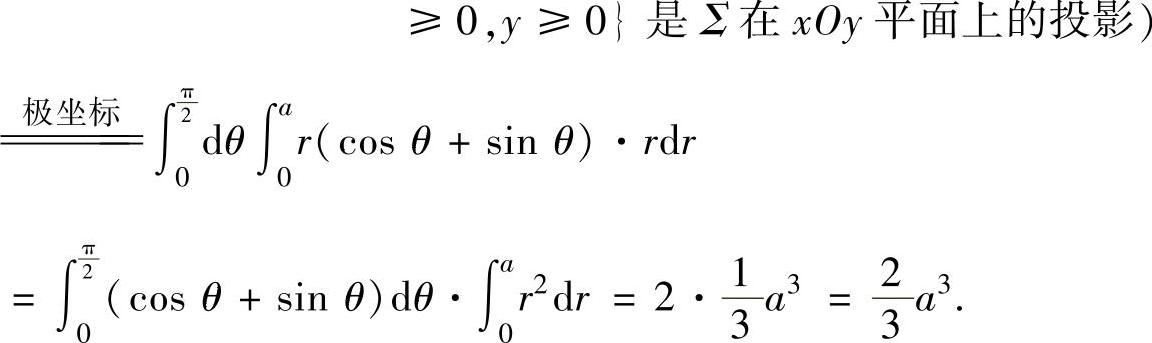
同样可以算出
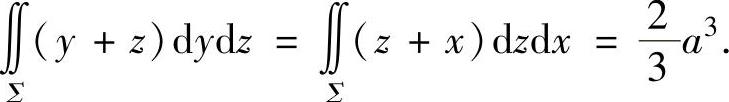
将它们代入式(2)得
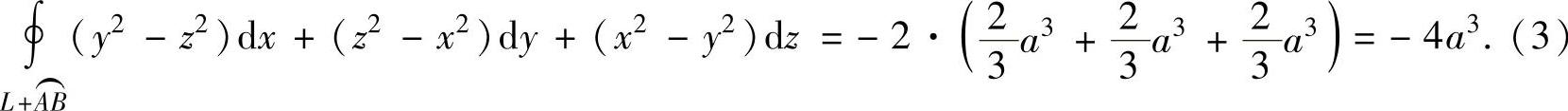
此外,由于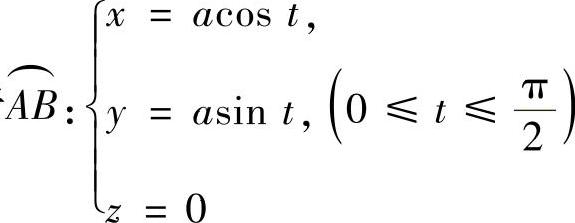 ,点A,B的参数分别对应
,点A,B的参数分别对应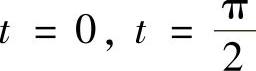 ,所以,
,所以, 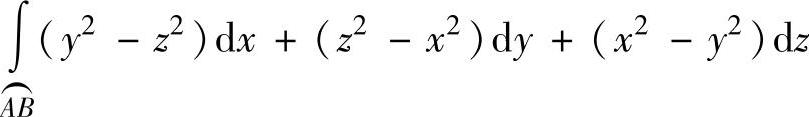
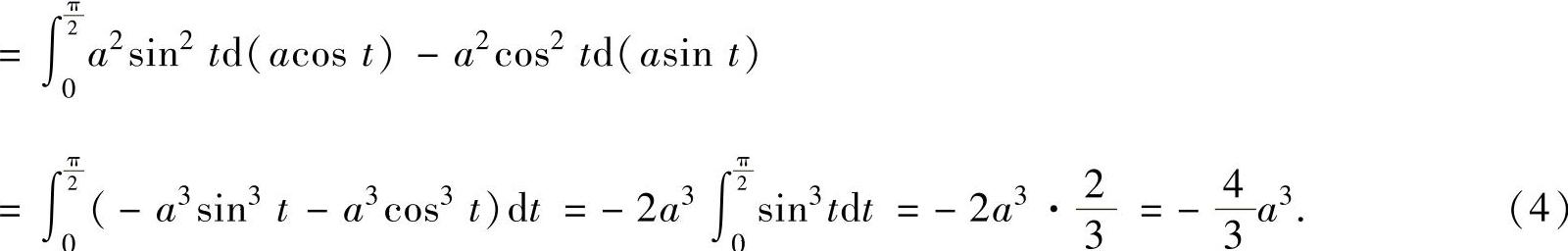 将式(3)、式(4)代入式(1)得
将式(3)、式(4)代入式(1)得
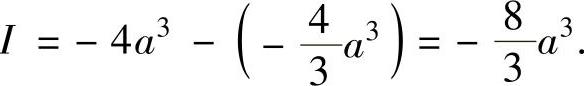
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




