高斯公式与散度及其应用

【主要内容】

1.高斯公式与散度

设三元函数P（x，y，z），Q（x，y，z），R（x，y，z）都有一阶连续偏导数，Ω是空间的有界的单连通或多连通闭区域，Σ为Ω的边界曲面（方向为外侧），则有

（高斯公式）（表示在外侧闭曲面Σ上的积分）.

记向量场A（x，y，z）=P（x，y，z）i+Q（x，y，z）j+R（x，y，z）k（其中P，Q，R都有连续偏导），则称

为A的散度.于是高斯公式也可以表示为

其中n⁰是有向曲面Σ上任一点处的单位法向量.

2.高斯公式应用的推广

应用高斯公式计算关于坐标的曲面积分的基本条件是：Σ是闭曲面，且P，Q，R都在Ω（即由Σ围成的空间闭区域）上有连续偏导数.但当这个条件不满足时，有时仍可间接使用高斯公式，具体方法如下：

（1）当Σ不是闭曲面（但P，Q，R都有连续偏导数）时，可以适当添上一块或几块曲面（记为Σ₁），使得Σ+Σ₁为闭曲面（不妨设其为外侧），并且使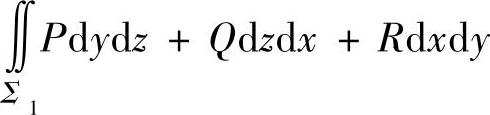比容易计算，于是对

的右边第一项应用高斯公式可较快地算出

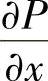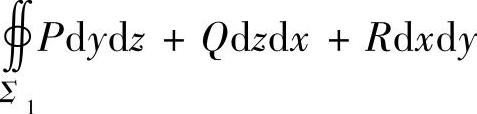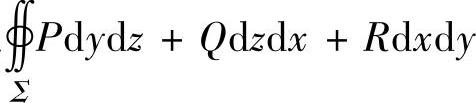（2）当，，或在由有向闭曲面围成的空间闭区域Ω内部有不连续点（x₀，y₀，z₀）时，可以作位于Ω内的闭曲面（记为Σ₁，外侧）将点（x₀，y₀，z₀）包围起来，Σ₁可以适当选取，使得比容易计算，于是对

（其中Σ₁-是Σ₁的反向曲面）对右边第一项应用高斯公式可较快地算出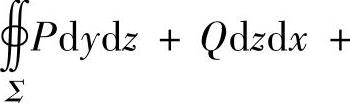

【典型例题】

例3.19.1 计算关于坐标的曲面积分

其中Σ是椭球面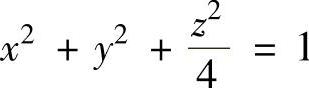的外侧.

精解 由于积分变量满足，即4x²+4y²+z²=4，因此

（注意：将Σ的方程代入到被积式中，对所给的曲面积分进行化简，是曲面积分计算中常用的方法）

（注意：椭球的体积故由Σ围成的空间闭区域的体积为.

例3.19.2 计算关于坐标的曲面积分

其中，Σ是曲面z=1-x²-y²（z≥0）的上侧.

精解 由于Σ不是闭曲面，因此如果要利用高斯公式计算本题，需添加一块曲面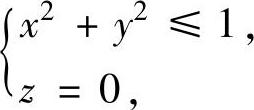下侧，使得Σ+Σ₁是闭曲面外侧.于是

其中，(www.xing528.com)

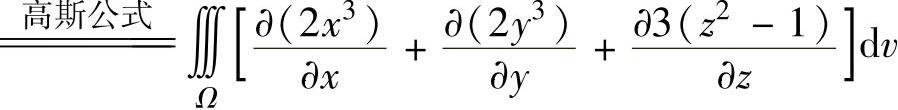（Ω是由Σ+Σ₁围成的空间闭区域，即Ω={（x，y，z）|（x，y）∈D_xy，0≤z≤1-x²-y²}）

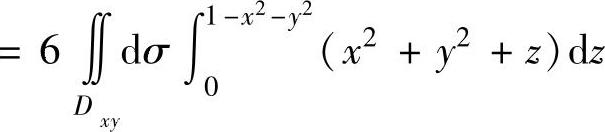（其中D_xy={（x，y）|x²+y²≤1}={（r，θ）|0≤r≤1，0≤θ≤2π}是Ω在xOy平面上的投影）

将式（2）、式（3）代入式（1）得

I=2π-3π=-π.

例3.19.3 计算关于坐标的曲面积分

其中Σ是包围坐标原点的光滑闭曲面的外侧.

精解 虽然Σ是闭曲面，但在Σ围成的空间闭区域内三元函数

都有不连续点（0，0，0），因此作小球面Σ₁：x²+y²+z²=ε²（ε是充分小正数，使得Σ₁位于Σ内部，方向取外侧），于是

其中 （其中Ω是由Σ+Σ₁ 围成的空间闭区域）

将式（2）、式（3）代入式（1）得

I=0+4π=4π.例3.19.4 求关于坐标的曲面积分

其中，Σ是上半球面（x-a）²+（y-b）²+（z-c）²=R²（z≥c，R>0）的上侧.

精解 先作坐标变换，将Σ的球心移到原点，然后考虑应用高斯公式.

令则Σ成为上半球面Σ₁：x²₁+y²₁+z²₁=R²（z₁≥0）的上侧，且

（其中Σ₀是平面z₁=0上圆域x²₁+y²₁≤R²的下侧）.显然Σ₁+Σ₀是外侧闭曲面，记它围成的空间闭区域为Ω，则Ω={（x₁，y₁，z₁）|x²₁+y²₁+z²₁≤R²，z₁≥0}，于是

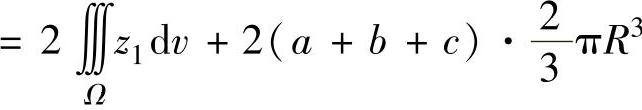（由于Ω关于平面x₁=0对称，在对称点处x₁的值互为相反数，所以，同样

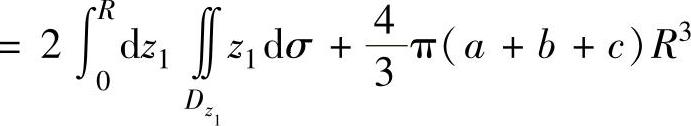（其中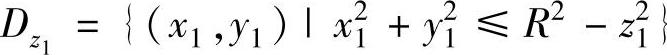是Ω的竖坐标为z₁的截面在xOy平面上的投影）

由于Σ₁：z₁=0，下侧，所以

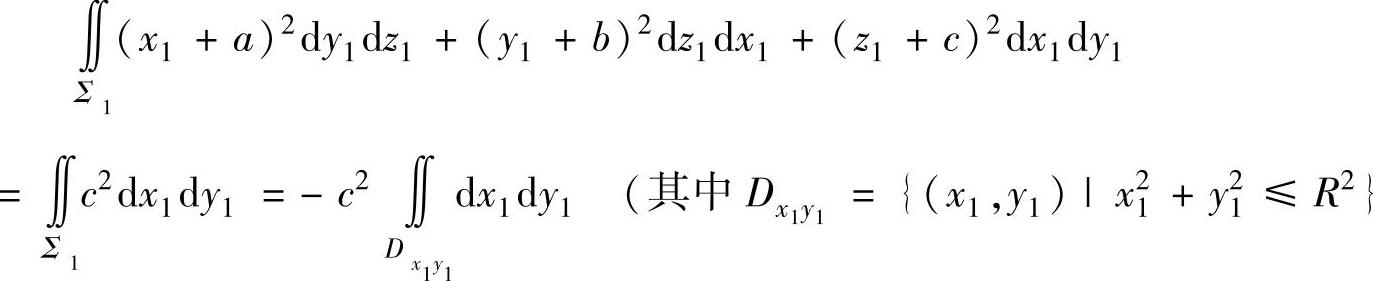是Σ₁在x₁Oy₁平面上的投影）

=-πc²R². （3）

将式（2）、式（3）代入式（1）得