【主要内容】
1.关于面积曲面积分的概念
设f(x,y,z)是有界函数,Σ:z=z(x,y)是光滑或分块光滑曲面,把Σ任意划分成n个小块:
ΔS1,ΔS2,…,ΔSn
其中ΔSi表示第i个小块,也表示该小块的面积(i=1,2,…,n).在每个小块ΔSi上任取一点(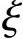 i,ηi,ζi)(i=1,2,…,n).如果不管Σ如何划分成n个小块,也不管在每个小块上如何取点,极限
i,ηi,ζi)(i=1,2,…,n).如果不管Σ如何划分成n个小块,也不管在每个小块上如何取点,极限
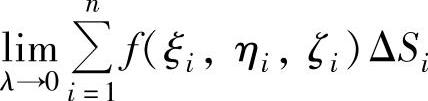 (其中λ是各小块中直径最大者)
(其中λ是各小块中直径最大者)
总是存在且相等,则称这个极限值为f(x,y,z)在Σ上的关于面积的曲面积分,记为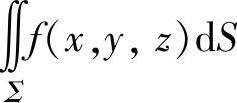 ,即
,即
当f(x,y,z)是连续函数时,关于面积的曲面积分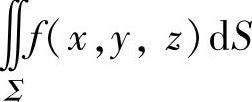 存在.
存在.
当f(x,y,z)=1时,f(x,y,z)在Σ上的关于面积的曲面积分即为S的面积.
2.关于面积曲面积分的计算方法
关于面积曲面积分可按以下步骤计算:
(1)按关于面积曲面积分的性质,尤其是关于积分曲面的对称性,化简所给的曲面积分,使它化为易于转化成二重积分的形式.
关于面积曲面积分主要有以下性质:
设f(x,y,z),g(x,y,z)都是连续函数,Σ是光滑或分块光滑曲面,则
(ⅳ)设S关于平面z=0(或x=0,或y=0)对称.如果在对称点处f(x,y,z)的值互为相反数,则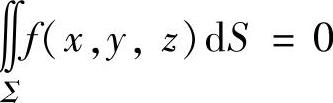 ;如果在对称点处f(x,y,z)的值彼此相等,则
;如果在对称点处f(x,y,z)的值彼此相等,则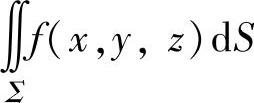
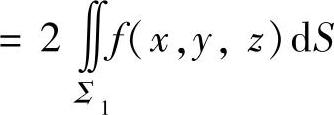 (其中Σ1是Σ按上述的对称性划分成的两部分之一).
(其中Σ1是Σ按上述的对称性划分成的两部分之一).
设S关于平面y=x对称(此时对称点为(x,y,z)与(y,x,z)).如果在对称点处f(x,y,z)的值互为相反数,则 ;如果在对称点处f(x,y,z)的值彼此相等,则
;如果在对称点处f(x,y,z)的值彼此相等,则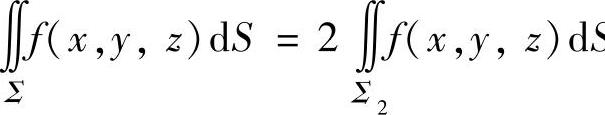 (其中Σ2是Σ按对称性划分成的两部分之一).
(其中Σ2是Σ按对称性划分成的两部分之一).
(2)将化简后的关于面积曲面积分(记为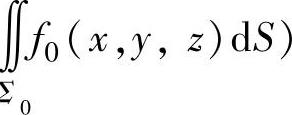 化为二重积分,然后计算这个二重积分,即可得到所求的关于面积曲面积分.
化为二重积分,然后计算这个二重积分,即可得到所求的关于面积曲面积分.
设f0(x,y,z)是连续函数,Σ0是光滑或分块光滑曲面.如果Σ0:z=z(x,y),则
其中,Dxy是Σ0在xOy平面上的投影;如果Σ0:x=x(y,z),则
其中,Dyz是Σ0在yOz平面上的投影;如果Σ0:y=y(x,z),则
其中,Dxz是Σ0在xOz平面上的投影.
如果Σ0的方程不能如以上那样用显函数表示,则需用一些与平面x=0(或y=0,或z=0)平行的平面,将Σ分成若干块,使每一块的方程都可用显函数表示,然后对每一块对应地使用以上所列公式,并将算出的曲面积分值逐一相加.
【典型例题】
例3.17.1 计算下列关于面积的曲面积分,其中Σ:x2+y2+z2=R2(R>0):(https://www.xing528.com)
精解 利用Σ的对称性计算本题.
(1)Σ关于平面x=0对称,在对称点处x的值互为相反数,所以
(2)由于Σ关于平面y=x对称,且在对称点(即(x,y,z)与(y,x,z))处y2-x2的值互为相反数,所以
同样有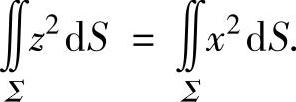 因此
因此
例3.17.2 求关于面积的曲面积分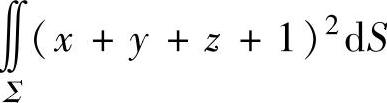 ,其中Σ是上半球面x2+y2+z2=R2(z≥0,常数R>0).
,其中Σ是上半球面x2+y2+z2=R2(z≥0,常数R>0).
精解 为了利用Σ的方程和Σ的对称性,需要改写曲面积分:
其中 
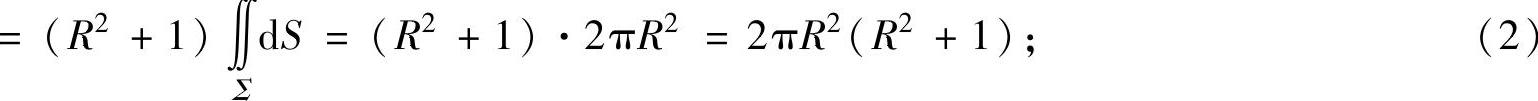
由于Σ关于平面x=0对称,在对称点处x(y+z+1)的值互为相反数,所以
由于Σ关于平面y=0对称,在对称点处y(z+1)的值互为相反数,所以
此外,
将式(2)~式(5)代入式(1)得
例3.17.3 计算关于面积的曲面积分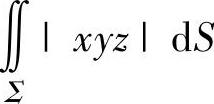 ,其中Σ是由曲面S1:z=x2+y2与曲面S2:z=1-x2-y2围成的立体表面.
,其中Σ是由曲面S1:z=x2+y2与曲面S2:z=1-x2-y2围成的立体表面.
精解 先利用Σ的对称性化简所给的曲面积分.
由于Σ既关于平面x=0对称,又关于平面y=0对称,且|xyz|在对称点处的值彼此相等,所以
其中Σ′是Σ位于第一卦限的部分,而S1′,S2′分别是Σ′的位于S1,S2上的部分,S1′与S2′的交线为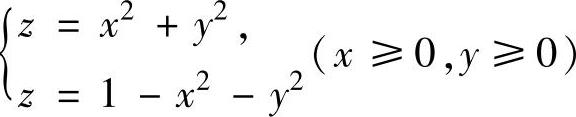 ,即
,即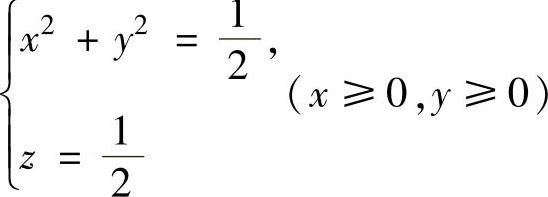 ,所以S1′,S2′在xOy平面上的投影同为
,所以S1′,S2′在xOy平面上的投影同为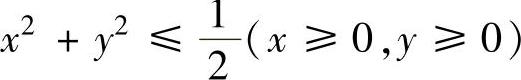 .于是
.于是
例3.17.4 设平面Πt:z=t(t≥0),求函数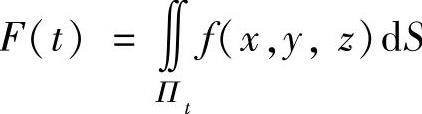 的表达式,其中
的表达式,其中
精解 根据平面Πt与球面Σ:x2+y2+z2=1的相对位置,即相交与不相交(包括相切)确定F(t)的表达式,而相交与不相交又由原点到平面Πt的距离t决定.
因此讨论0≤t<1与t≥1来计算F(t)的表达式.
当0≤t<1时,Πt与Σ相交,记Πt在Σ里的部分为Σt,它在xOy平面上的投影Dxy为由曲线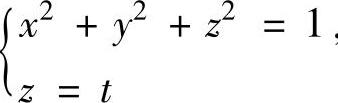 ,在xOy平面的投影x2+y2=1-t2围成的区域,即Dxy={(x,y)|x2+y2≤1-t2},所以,
,在xOy平面的投影x2+y2=1-t2围成的区域,即Dxy={(x,y)|x2+y2≤1-t2},所以,
(由于Σt:z=t,所以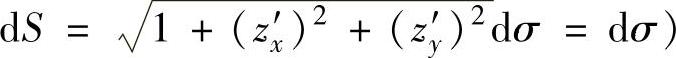
当t≥1时,Πt与Σ不相交(包括相切),所以
综上所述,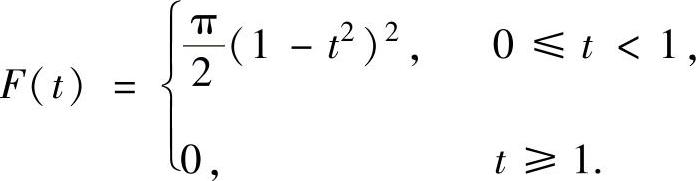
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




