【主要内容】
1.格林公式
设D是以光滑或分段光滑的平面曲线C为边界的单连通或多连通闭区域.二元函数P(x,y),Q(x,y)都在D上有连续偏导数,则

(注意:上式的 表示沿正向闭曲线C的积分).
表示沿正向闭曲线C的积分).
应用格林公式计算关于坐标曲线积分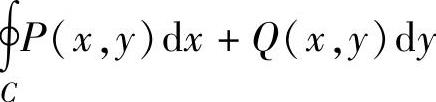 的基本条件是:C是闭曲线,且
的基本条件是:C是闭曲线,且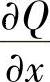 ,
,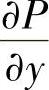 在D(即由C围成的闭区域)上连续,但当基本条件不满足时,有时仍可间接使用格林公式,具体如下:
在D(即由C围成的闭区域)上连续,但当基本条件不满足时,有时仍可间接使用格林公式,具体如下:
(1)当C不是闭曲线(但P,Q都有一阶连续偏导数)时,可以适当添上一条或几条曲线(记为C1),使得C+C1为闭曲线(不妨设为正向闭曲线,且记其围成的闭区域为D1),并且使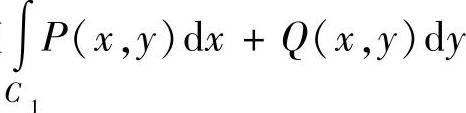 较
较 容易计算.于是对
容易计算.于是对

的右边第一项应用格林公式可较快地算出
(2)当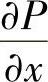 ,
, 在D的内部某点处不连续时,可以作位于D内部的正向闭曲线(记为C2)将该不连续点包围起来,则
在D的内部某点处不连续时,可以作位于D内部的正向闭曲线(记为C2)将该不连续点包围起来,则

于是对等式右边第一项可使用格林公式
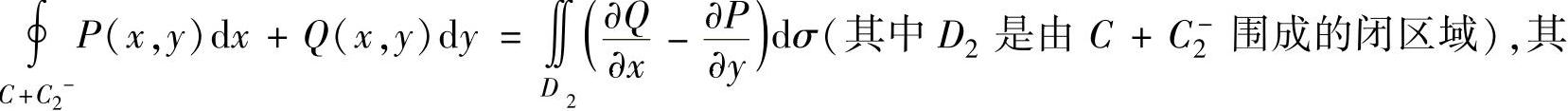
中,C-2是C2的反向闭曲线.对于第二项可以将C2的参数方程代入然后转换成定积分来计算,由此算出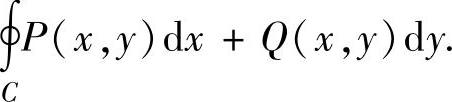
2.曲线积分与路径无关的条件
设G是单连通区域,P(x,y),Q(x,y)在G内具有连续偏导数,则关于坐标的曲线积分在G内与路径无关的充分必要条件是
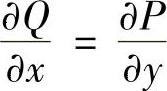
在G内成立.
此时, ,
,
其中,u(x,y)是全微分为P(x,y)dx+Q(x,y)dy的任一函数.
【典型例题】
例3.16.1 求关于坐标的曲线积分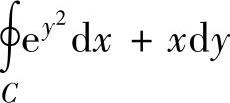 ,其中C是正向椭圆4x2+y2=8x.
,其中C是正向椭圆4x2+y2=8x.
精解 由于C是正向闭曲线,所以用格林公式计算所给的曲线积分.
C的方程可以写成4(x-1)2+y2=4,即( ,记由正向闭曲线C围成的闭区域为D,则由格林公式得
,记由正向闭曲线C围成的闭区域为D,则由格林公式得
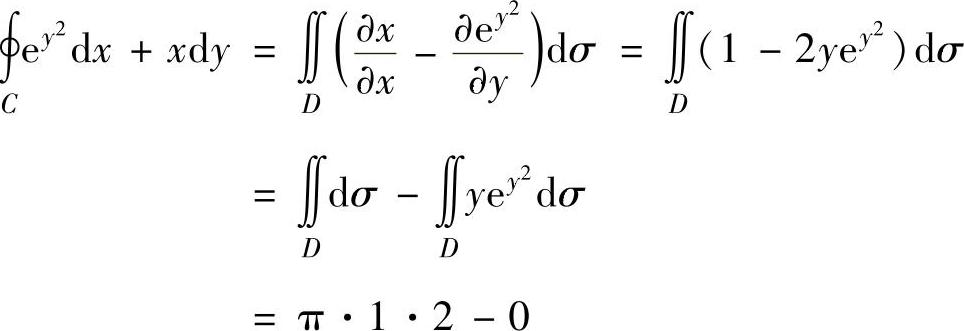
(由于D关于x轴对称,yey2在对称点处的值互为相反数,所以∬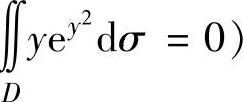

例3.16.2 求关于坐标的曲线积分 ,其中
,其中 是曲线y=sinx上从原点O(0,0)到点A(π,0)的弧段.
是曲线y=sinx上从原点O(0,0)到点A(π,0)的弧段.
精解 为了应用格林公式计算所给的曲线积分,应在 上添上线段
上添上线段 ,构成正向闭曲线,记其围成的闭区域为D,则
,构成正向闭曲线,记其围成的闭区域为D,则
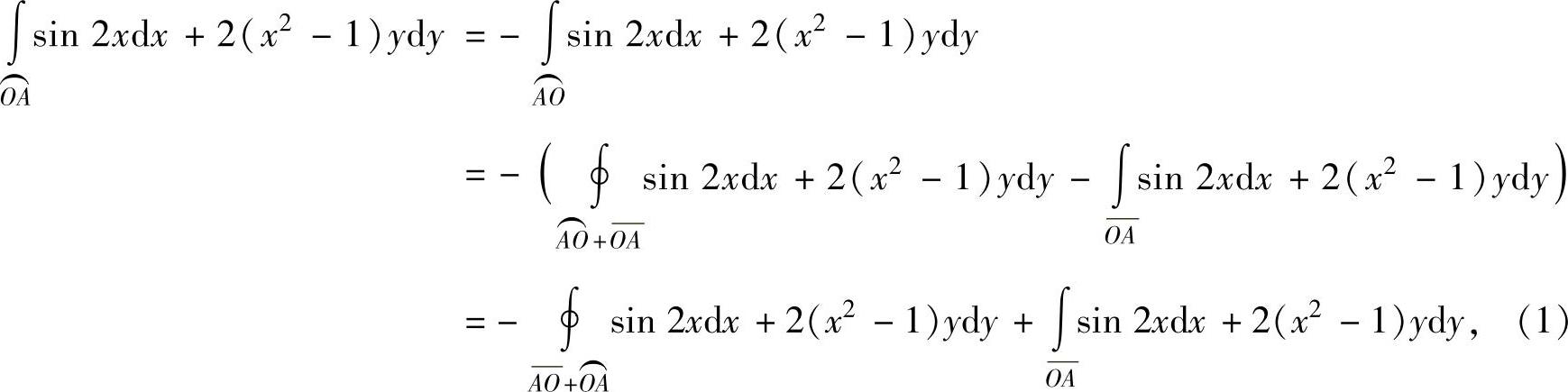
其中 
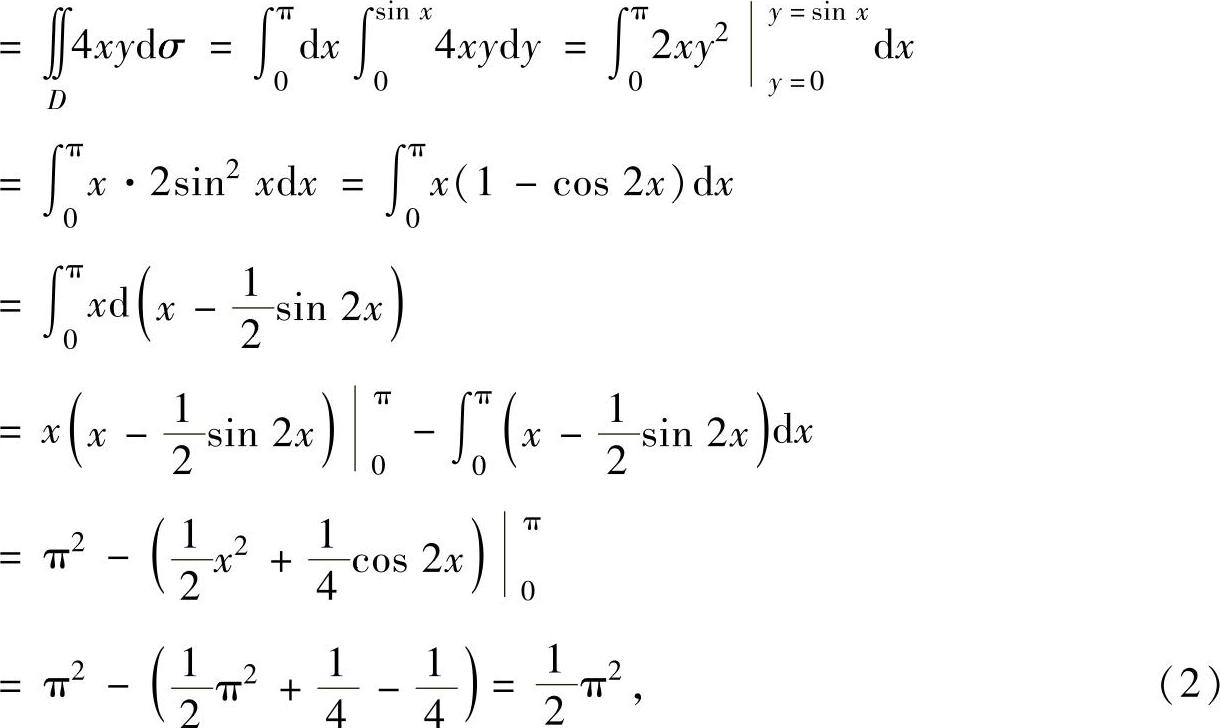

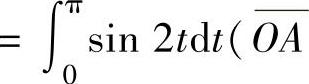 的参数方程
的参数方程 及O,A的参数分别为t=0,t=π)
及O,A的参数分别为t=0,t=π)

将式(2)、式(3)代入式(1)得
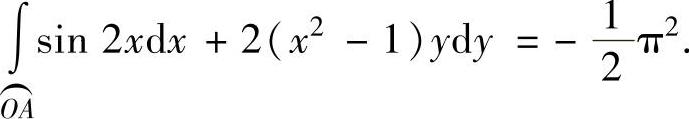
例3.16.3 求关于坐标的曲线积分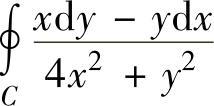 ,其中C是以(1,0)为中心,R(R>1)为半径的正向圆周.
,其中C是以(1,0)为中心,R(R>1)为半径的正向圆周.
精解 显然在以C为边界的闭区域D内
 ,
, 有不连续点(0,0),因此为了应用格林公式需作正向闭曲线Cε:4x2+y2=ε2(其中ε是充分小的正数,使Cε位于C之内),如图3.16.3所示.
有不连续点(0,0),因此为了应用格林公式需作正向闭曲线Cε:4x2+y2=ε2(其中ε是充分小的正数,使Cε位于C之内),如图3.16.3所示.
则以C+C-ε(C-ε-是Cε的反向曲线)为边界的闭区域Dε内有
 (https://www.xing528.com)
(https://www.xing528.com)
图 3.16.3

即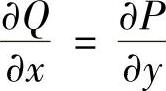 ,所以
,所以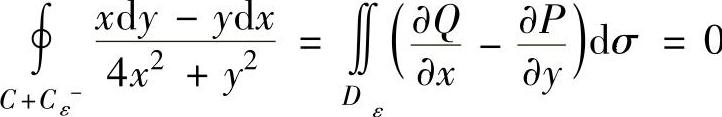 ,从而
,从而

(Cε的参数方程为 且起点、终点参数分别为
且起点、终点参数分别为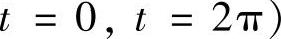
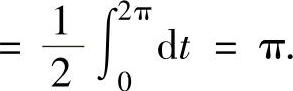
注 把Cε的方程取为4x2+y2=ε2,是为了使 化简成
化简成 应注意类似的处理方法.
应注意类似的处理方法.
例3.16.4 设函数φ(y)连续可导,在围绕原点的任意分段光滑正向闭曲线L上,关于坐标的曲线积分

的值恒为同一常数.
(1)证明:对右半平面内的任意分段光滑正向闭曲线C有
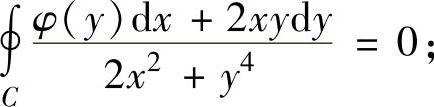
(2)求函数φ(y)的表达式.
精解 (1)设C如图3.16.4所示,将它分成C1与C2两部分,分点为A,B,以A为起点B为终点作一光滑或分段光滑的曲线C3,使得C1+C3,C2+C-3(C3-是C3的反向曲线)都是围绕原点的闭曲线,如图3.16.4所示,则

图 3.16.4

于是
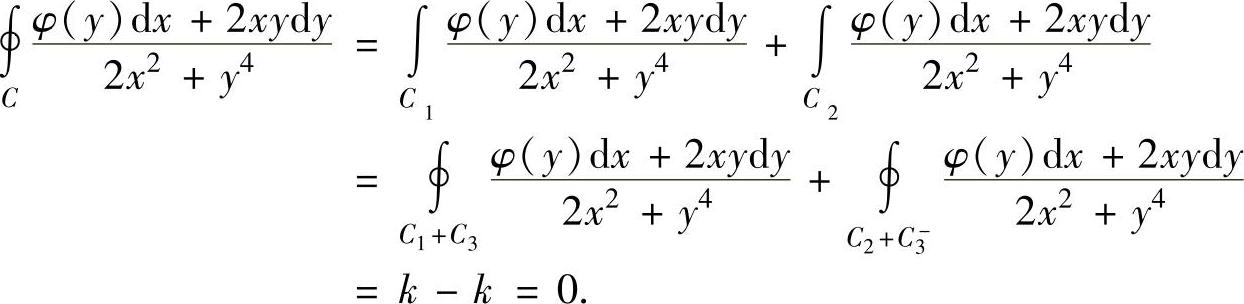
(2)由(1)知,在右半平面上有

所以由式(1)得
2y5-4x2y=φ′(y)(2x2+y4)-4y3φ(y),
即 2y5+4y3φ(y)-y4φ′(y)=2x2[φ′(y)+2y].
由于上式对任何x>0都成立,所以有
2y5+4y3φ(y)-y4φ′(y)=0, (2)
φ′(y)+2y=0. (3)
将式(3)代入式(2)得φ(y)=-y2.
例3.16.5 设函数f(x)连续可导,L是上半平面y>0上分段光滑的有向曲线,其起点为(a,b),终点为(c,d),记
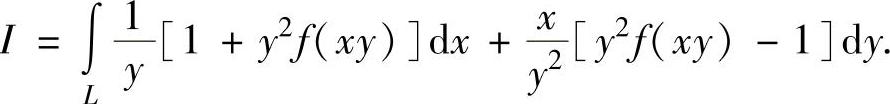
(1)证明I与积分路径L无关;
(2)当ab=cd时,求I的值.
精解 (1)由于在上半平面上有

即 
所以I与上半平面上的路径L无关.
(2)由(1)知存在二元函数u(x,y),使得

所以,可取 .于是
.于是
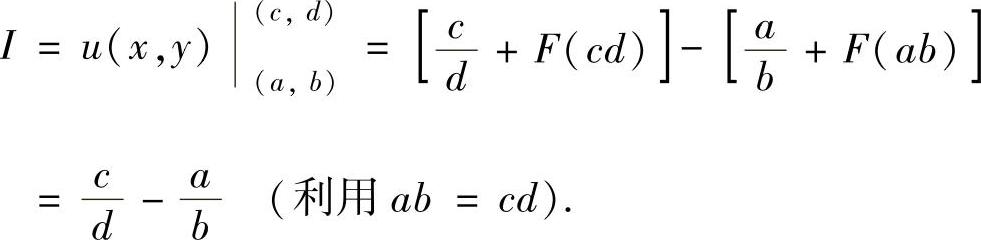
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




