【主要内容】
1.二重积分的概念
设二元函数f(x,y)在xOy平面有界闭区域D上有界,将D任意划分成n个小闭区域Δσ1,Δσ2,…,Δσn,其中Δσi表示第i个小闭区域,也表示它的面积,在每个小闭区域Δσi上任取一点(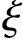 i,ηi)(i=1,2,…,n),如果不管如何划分Δσ1,Δσ2,…,Δσn,也不管在每个Δσi上如何取点(
i,ηi)(i=1,2,…,n),如果不管如何划分Δσ1,Δσ2,…,Δσn,也不管在每个Δσi上如何取点(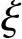 i,ηi),极限
i,ηi),极限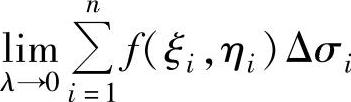 (其中,λ表示各个小区域Δσi的直径的最大者)总是存在且相等,则称此极限值为f(x,y)在D上的二重积分,记为
(其中,λ表示各个小区域Δσi的直径的最大者)总是存在且相等,则称此极限值为f(x,y)在D上的二重积分,记为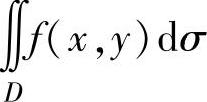 ,即
,即
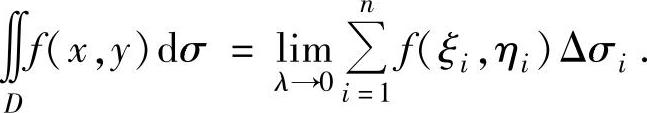
当f(x,y)是有界闭区域D上的二元连续函数时,二重积分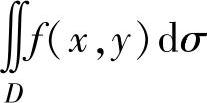 存在,并且当f(x,y)≥0时,
存在,并且当f(x,y)≥0时,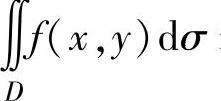 表示以D为底,曲面z=f(x,y)为顶,侧面是以D的边界为准线、母线平行于z轴的柱面所围成的曲顶柱体的体积.
表示以D为底,曲面z=f(x,y)为顶,侧面是以D的边界为准线、母线平行于z轴的柱面所围成的曲顶柱体的体积.
2.二重积分的计算方法
有界闭区域上二元连续函数的二重积分计算步骤如下:
(1)按二重积分的性质,尤其是利用积分区域的对称性,化简二重积分,使它转化成易于化为二次积分的形式.
二重积分主要有以下性质:
设f(x,y),g(x,y)都是有界闭区域D上的连续函数,k是常数,则
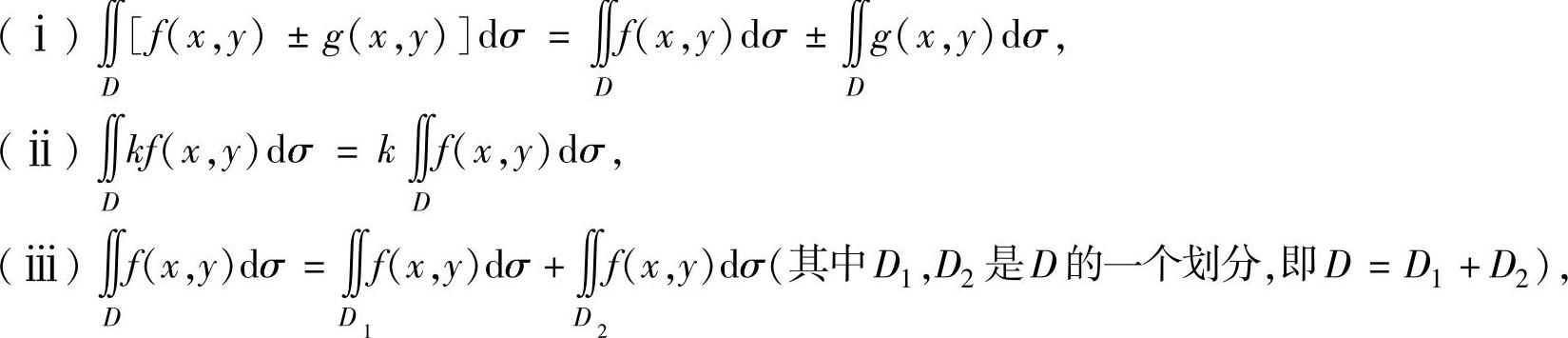
(ⅳ)对于二重积分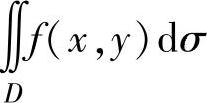 ,当D关于x轴(或y轴)对称时,如果在对称点处f(x,y)的值互为相反数,则
,当D关于x轴(或y轴)对称时,如果在对称点处f(x,y)的值互为相反数,则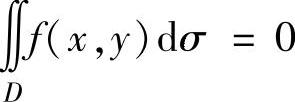 ;如果f(x,y)的值彼此相等,则
;如果f(x,y)的值彼此相等,则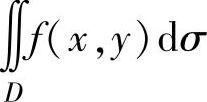
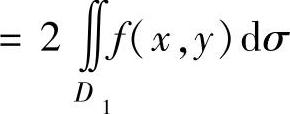 ,其中D1是D按对称性划分而成的两部分之一.
,其中D1是D按对称性划分而成的两部分之一.
当D既关于x轴对称,又关于y轴对称时,如果在对称点处f(x,y)的值彼此相等,则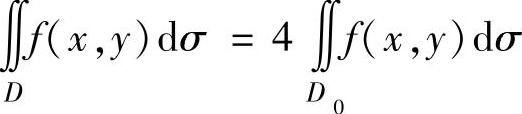 (D0是D按对称性划分成的四部分之一).
(D0是D按对称性划分成的四部分之一).
(2)将化简后的二重积分记为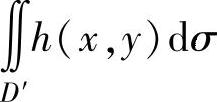 ,然后进行两次定积分计算,即算得所求的二重积分值.将二重积分
,然后进行两次定积分计算,即算得所求的二重积分值.将二重积分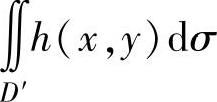 化为二次积分的方法具体如下:
化为二次积分的方法具体如下:
(ⅰ)设D′={(x,y)|a≤x≤b,φ1(x)≤y≤φ2(x)}(称为X型),则
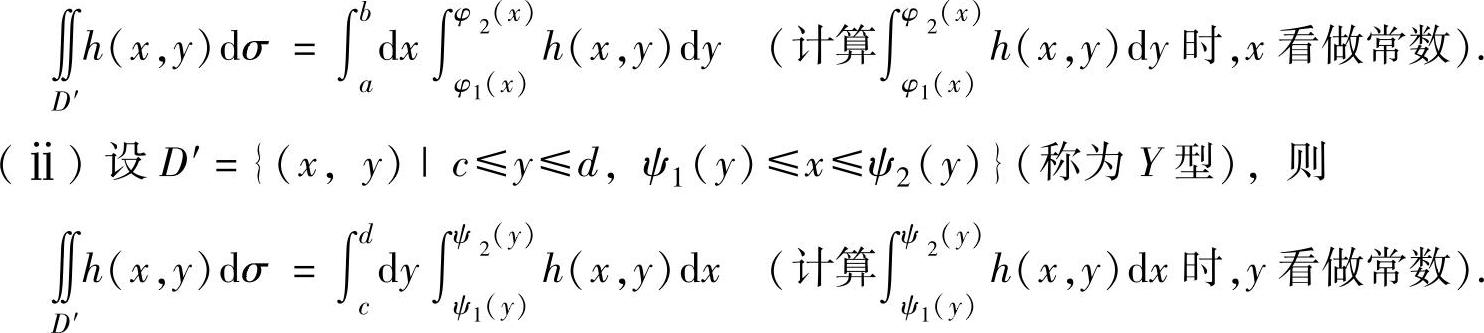
(ⅲ)设D′={(r,θ)|0≤α≤θ≤β≤2π,r1(θ)≤r≤r2(θ)}(角域型),则
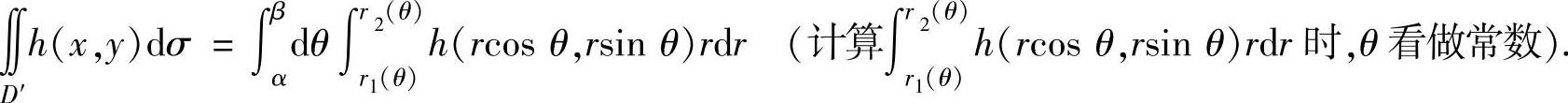
(ⅳ)当D′既不是X型,也不是Y型和角域型时,需用与y轴平行的直线,或与x轴平行的直线,或从原点发出的射线将D′分成若干小块X型,或Y型,或角域型,然后对各小块应用(ⅰ),或(ⅱ),或(ⅲ).
【典型例题】
例3.10.1 设f(x,y)是二元连续函数,且满足
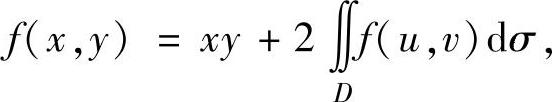 其中,D是由直线y=0,x=1和曲线y=x2围成的闭区域.求f(x,y)的表达式.
其中,D是由直线y=0,x=1和曲线y=x2围成的闭区域.求f(x,y)的表达式.
精解 由于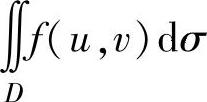 是常数,记为A,则所给等式成为
是常数,记为A,则所给等式成为
f(x,y)=xy+2A. (1)
式(1)两边在D(如图3.10.1阴影部分所示)积分得
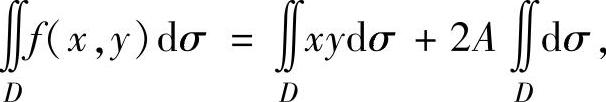
即

由于D={(x,y)|0≤x≤1,0≤y≤x2}是X型,所以
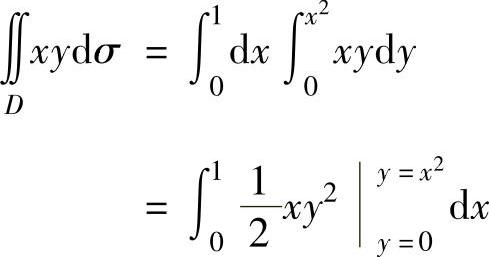
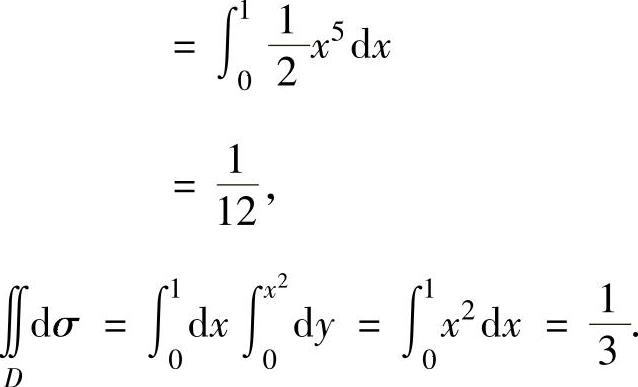
将它们代入式(2)得
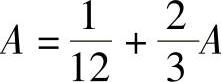 , 即
, 即 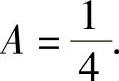
将它代入式(1)得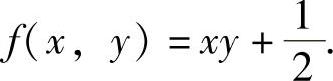
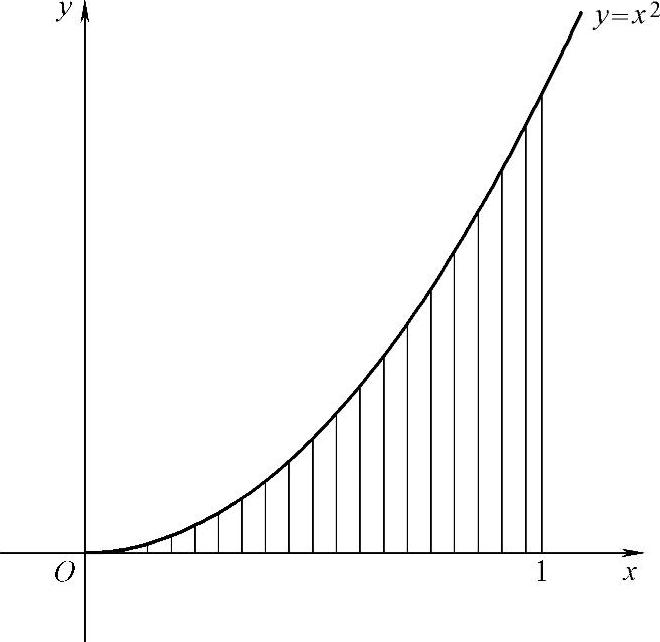
图 3.10.1
例3.10.2 求二重积分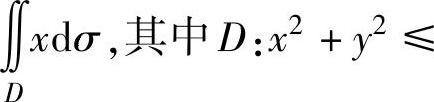
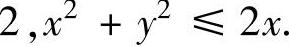
精解 D如图3.10.2阴影部分所示,它可表示为
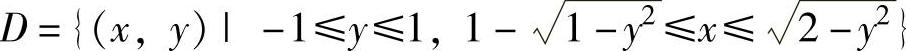 ,显然是Y型,所以
,显然是Y型,所以
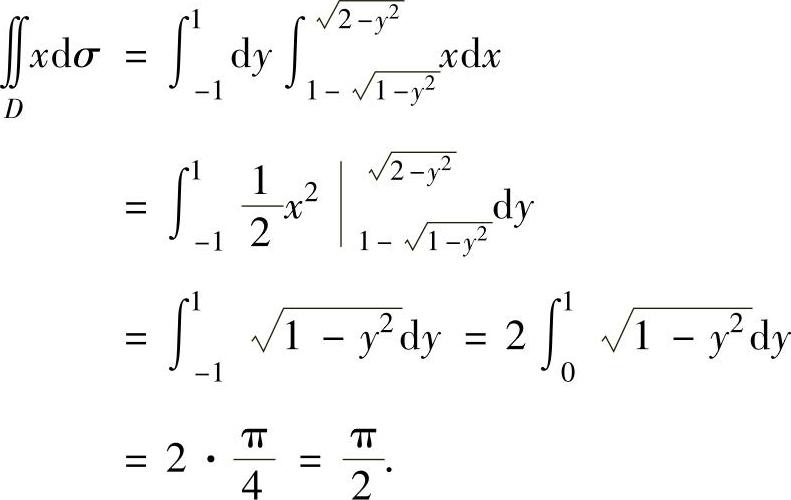
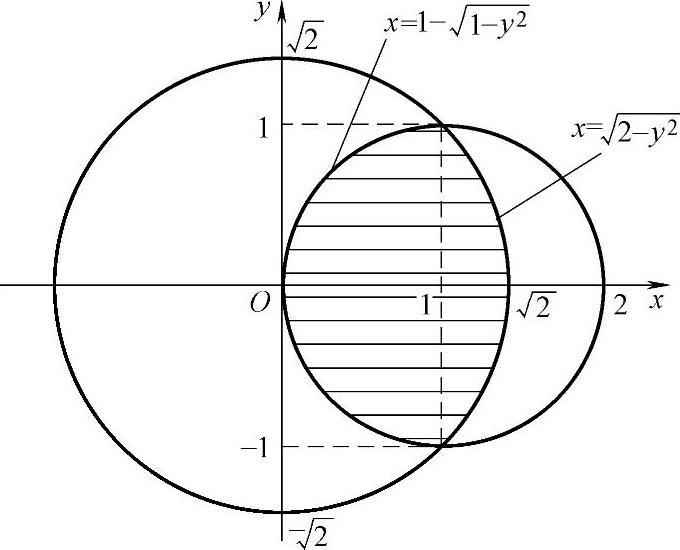
图 3.10.2(https://www.xing528.com)
例3.10.3 计算二重积分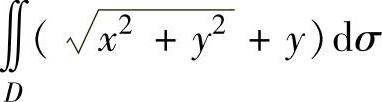 ,其中D:x2+y2≤4和(x+1)2+y2≥1.
,其中D:x2+y2≤4和(x+1)2+y2≥1.
精解 D如图3.10.3阴影部分所示,所以

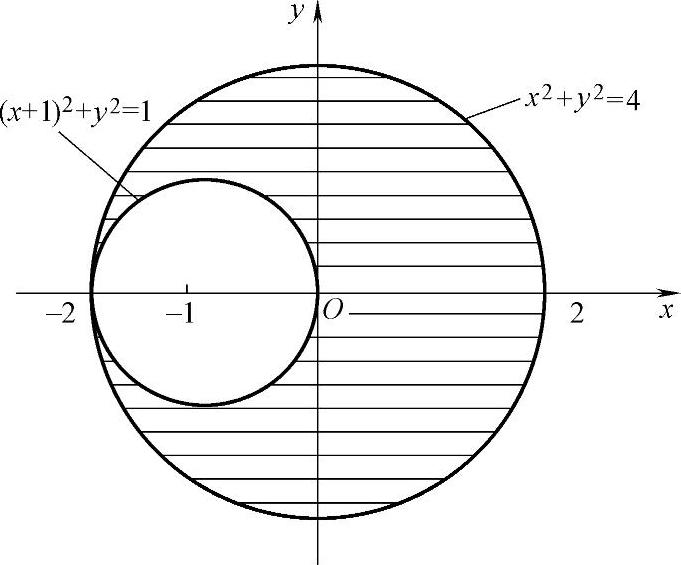
图 3.10.3
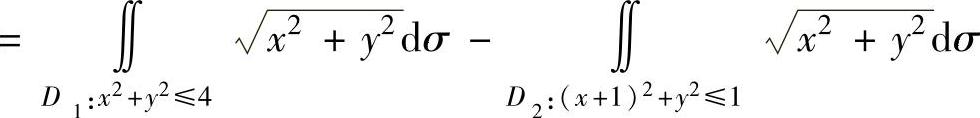
(由于D的图形比较复杂,不易计算二重积分,但它是D1与D2之差,而D1与D2都是圆,它们的二重积分比较容易计算,因此将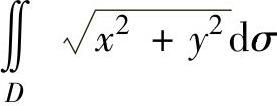 表示成
表示成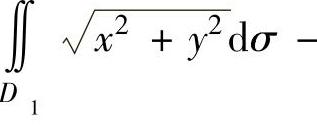
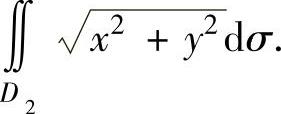 这种方法在二重积分中是有用的,应予以注意)
这种方法在二重积分中是有用的,应予以注意)

例3.10.4 设二元函数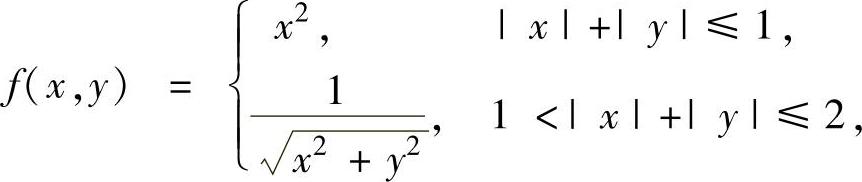 求二重积分
求二重积分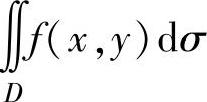 ,其中D={(x,y)|x|+|y|≤2}.
,其中D={(x,y)|x|+|y|≤2}.
精解 D关于x轴对称,也关于y轴对称,f(x,y)在对称点处的函数值彼此相等,所以,
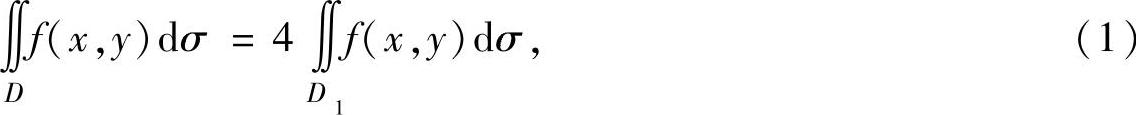
其中D1是D在第一象限的部分.
按f(x,y)的表达式,将D1划分成D11与D12两块,如图3.10.4所示.
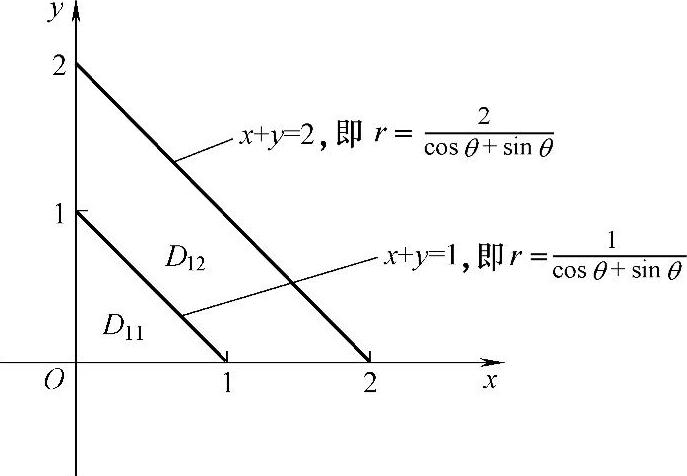
图 3.10.4
D11={(x,y)|x+y≤1,x≥0,y≥0},
D12={(x,y)|1<x+y≤2,x≥0,y≥0}.
于是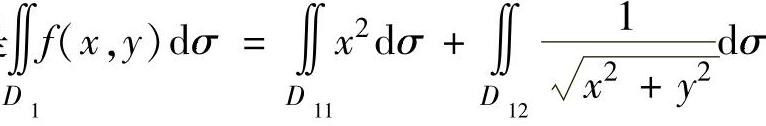 ,(2)
,(2)
其中, 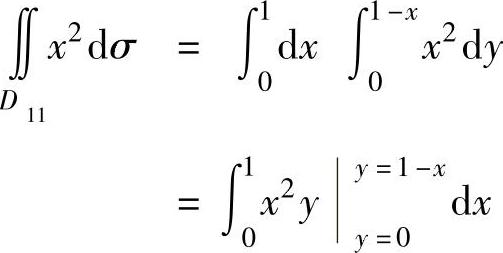
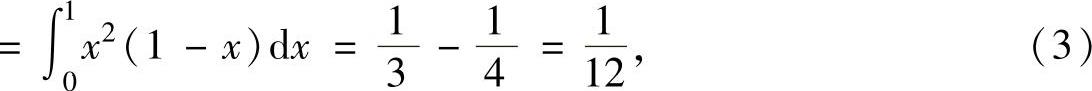
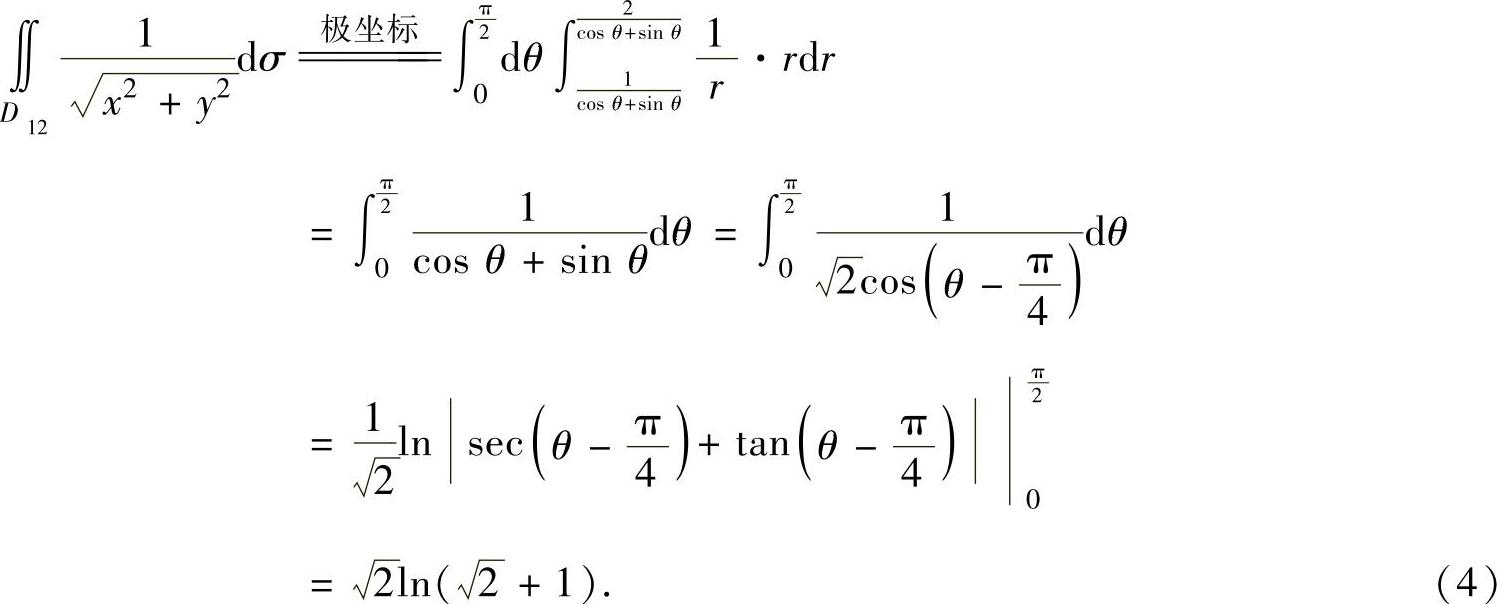
将式(3)和式(4)代入式(2)得
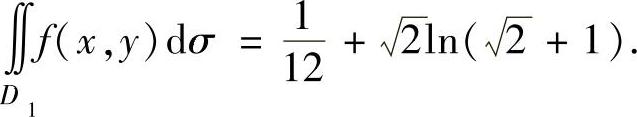
从而由式(1)知
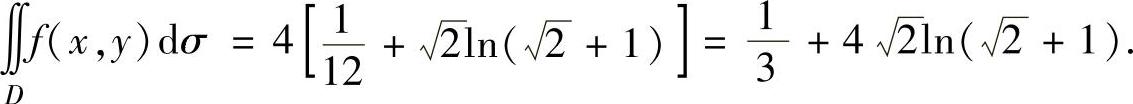
例3.10.5 求二重积分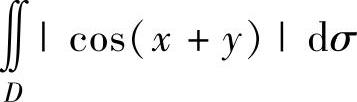 ,其中D={(x,y)|0≤x≤π,0≤y≤π}.
,其中D={(x,y)|0≤x≤π,0≤y≤π}.
精解 因为
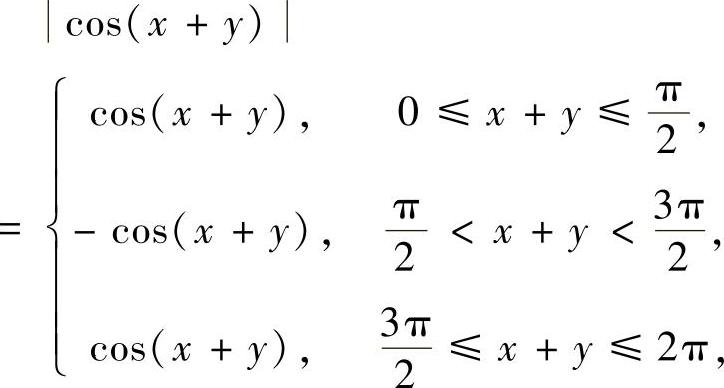
所以用直线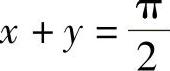 ,
,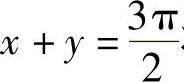 将D划分成D1、D2、D3,即
将D划分成D1、D2、D3,即
D=D1+D2+D3,
如图3.10.5所示.于是
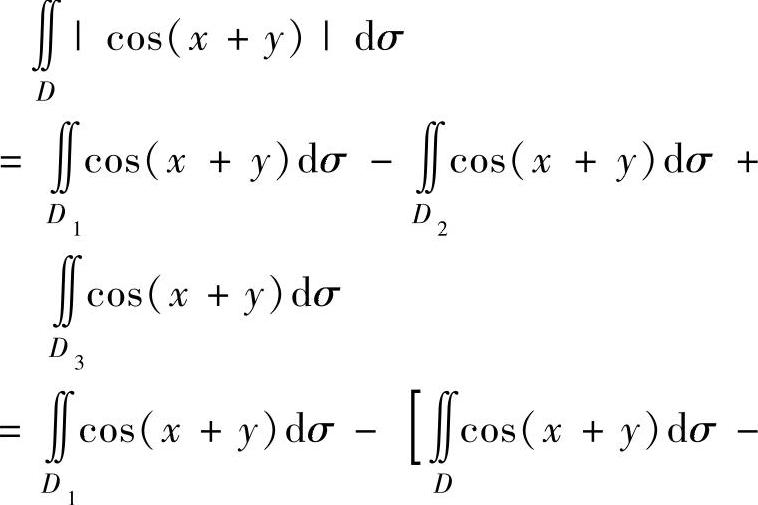
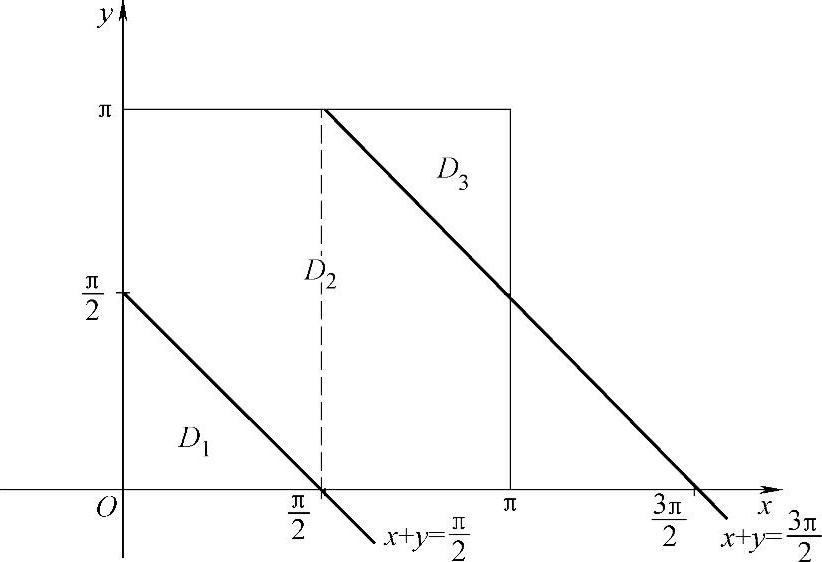
图 3.10.5
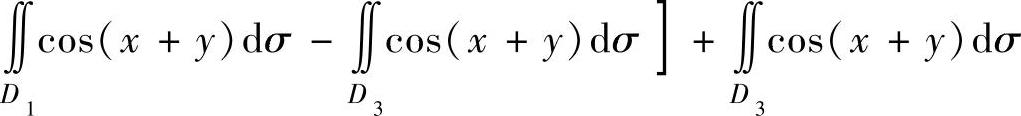
(这里,由于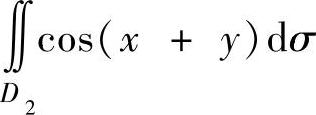 不易直接计算,故把它转换成
不易直接计算,故把它转换成
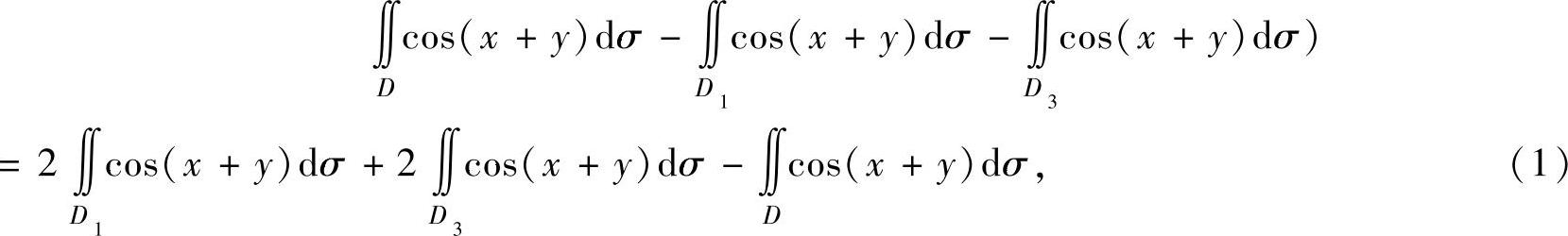
其中,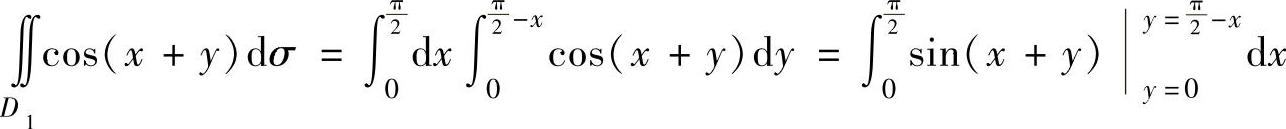
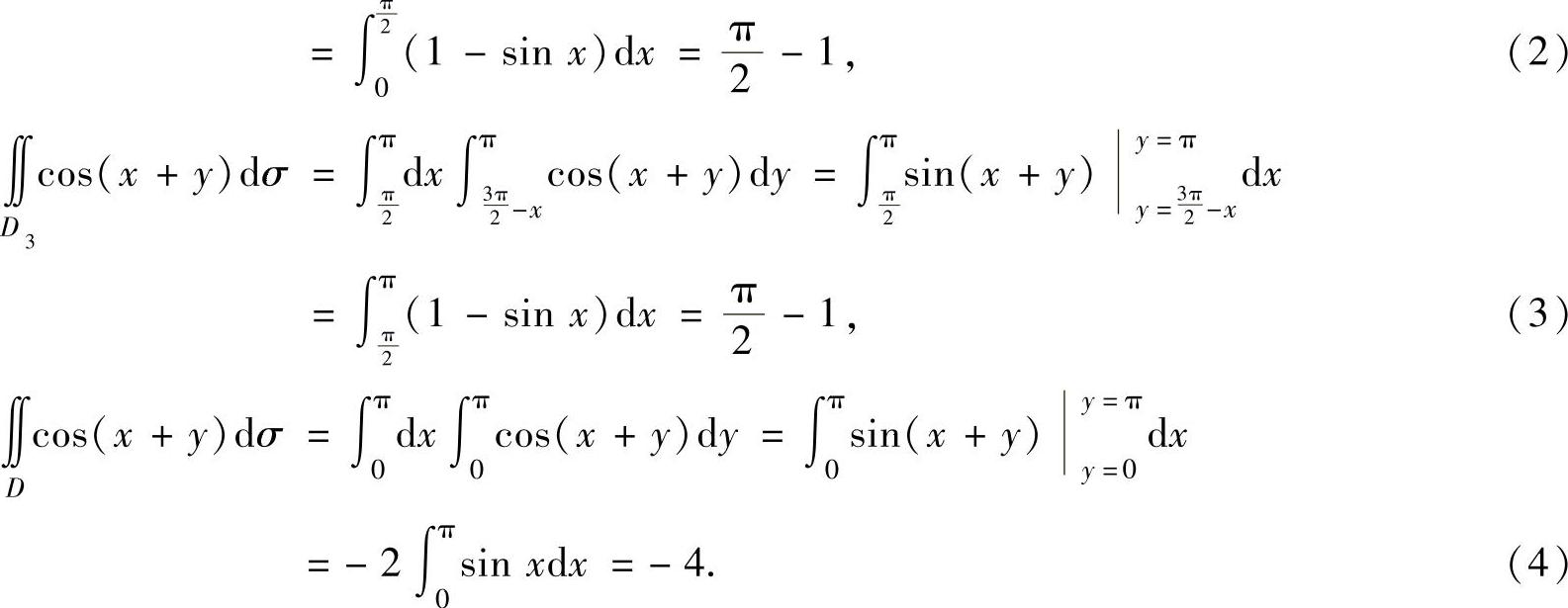 将式(2)、式(3)、式(4)代入式(1)得
将式(2)、式(3)、式(4)代入式(1)得
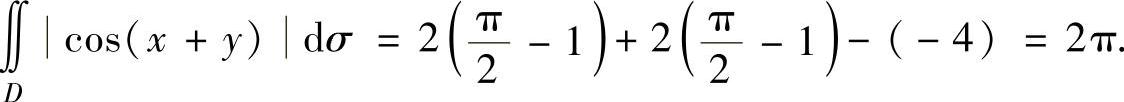
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




