【主要内容】
1.二元函数情形
二元函数f(x,y)在约束条件φ(x,y)=0下的极值,称为条件极值,其中f(x,y)称为目标函数.
设f(x,y),φ(x,y)都具有二阶连续偏导数,则上述的条件极值可利用拉格朗日乘数法计算,具体步骤如下:
(1)作拉格朗日函数F(x,y,λ)=f(x,y)+λφ(x,y)(其中λ是非零常数).
(2)求解方程组
(3)检验.上述方程组的每个解都是f(x,y)在约束条件φ(x,y)=0下的可能极值点,逐一检验f(x,y)在各个可能极值点处是否取到极大值或极小值.通常条件极值问题中计算的是最值,它可按以下方法直接得到:
如果只有一个可能极值点(x1,y1),则f(x1,y1)就是f(x,y)在φ(x,y)=0下的最值,至于是最大值还是最小值可按问题的实际意义确定;
如果有可能极值点(x1,y1),(x2,y2),…,(xn,yn),则
f(x,y)在φ(x,y)=0下的最大值=max{f(x1,y1),f(x2,y2),…,f(xn,yn)},
f(x,y)在φ(x,y)=0下的最小值=min{f(x1,y1),f(x2,y2),…,f(xn,yn)}.
2.三元函数情形
三元函数f(x,y,z)在约束条件φ(x,y,z)=0或φ1(x,y,z)=0与φ2(x,y,z)=0下的极值称为条件极值,其中f(x,y,z)称为目标函数.
设f(x,y,z),φ(x,y,z),φ1(x,y,z),φ2(x,y,z)都具有二阶连续偏导数,则上述的条件极值可用拉格朗日乘数法计算,具体步骤如下:
(1)作拉格朗日函数
F(x,y,z,λ)=f(x,y,z)+λφ(x,y,z) (λ是非零常数),
或G(x,y,z,λ,μ)=f(x,y,z)+λφ1(x,y,z)+μφ2(x,y,z) (λ,μ是不全为零常数).
(2)求解方程组
(3)检验.与二元函数情形相同.
【典型例题】
例3.8.1 (单项选择题)设f(x,y),φ(x,y)都是可微函数,且φy′(x,y)≠0.已知(x0,y0)是f(x,y)在约束条件φ(x,y)=0下的一个极值点,则下列选项中正确的是( ).
A.若fx′(x0,y0)=0,则fy′(x0,y0)=0
B.若fx′(x0,y0)=0,则fy′(x0,y0)≠0
C.若fx′(x0,y0)≠0,则fy′(x0,y0)=0
D.若fx′(x0,y0)≠0,则fy′(x0,y0)≠0
精解 利用拉格朗日乘数法可得正确选项.
记F(x,y,λ)=f(x,y)+λφ(x,y),并记对应点(x0,y0)的λ值为λ0,则由题设知(x0,y0)是f(x,y)在φ(x,y)=0下的一个极值点.所以
消去其中的λ0得fx′(x0,y0)φy′(x0,y0)-fy′(x0,y0)φx′(x0,y0)=0.
由此可知,当fx′(x0,y0)≠0时,由φy′(x0,y0)≠0得fy′(x0,y0)≠0.
因此本题选D.
例3.8.2 求二元函数z=x2+y2+5在约束条件y=1-x下的极值.(https://www.xing528.com)
精解 由于是计算z在y=1-x下的极值,所以将y=1-x代入z,转换成一元函数,再计算极值.
将y=1-x代入z得
z=x2+(1-x)2+5=2x2-2x+6.
由于 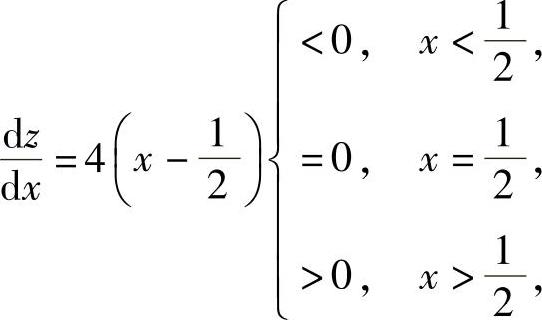 所以z=2x2-2x+6在
所以z=2x2-2x+6在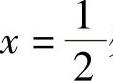 处取得极小值.因此,二元函数z=x2+y2+5在约束条件y=1-x下有极小值
处取得极小值.因此,二元函数z=x2+y2+5在约束条件y=1-x下有极小值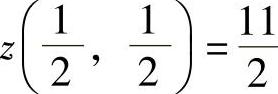 ,无极大值.
,无极大值.
例3.8.3 求二元函数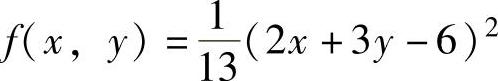 在约束条件x2+4y2=4下的极值.
在约束条件x2+4y2=4下的极值.
精解 用拉格朗日乘数法求解.
记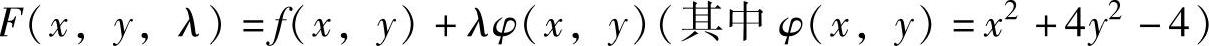
则 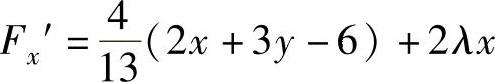 ,
,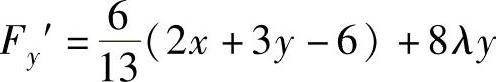 .于是方程组
.于是方程组
由式(1)和式(2)消去λ得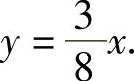 代入式(3)得
代入式(3)得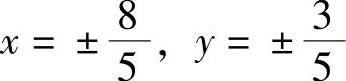 ,即f(x,y)在约束条件φ(x,y)=0下的可能极值点为
,即f(x,y)在约束条件φ(x,y)=0下的可能极值点为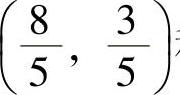 和
和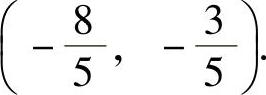
下面判别它们是否为极值点.
x2+4y2=4的两边对x求导得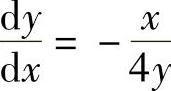 .于是
.于是
由此得到
所以,f(x,y)在约束条件φ(x,y)=0下,有极小值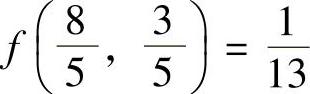 ,有极大值
,有极大值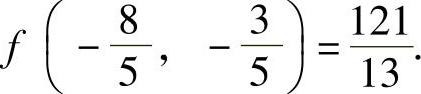
例3.8.4 将正数a分为三个小正数之和,使它们的乘积为最大,求这三个小正数.
精解 设三个小正数为x,y,z,则本题即为在约束条件x+y+z=a下计算三元函数z=xyz(0<x<a,0<y<a,0<z<a)的最小值,故可应用拉格朗日乘数法.
记F(x,y,z,λ)=xyz+λ(x+y+z-a),
则 Fx′=yz+λ,Fy′=xz+λ,Fz′=xy+λ.于是方程组
由式(1)、式(2)和式(3)知x=y=z.将它代入式(4)得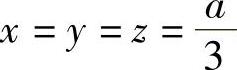 ,即xyz在x+y+z=a下只有一个可能极值点
,即xyz在x+y+z=a下只有一个可能极值点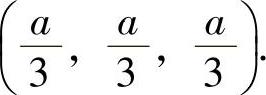
由于现在要计算的是约束条件下的最大值,因此它必在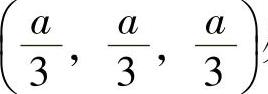 处取到,即乘积为最大的三个小正数应都为
处取到,即乘积为最大的三个小正数应都为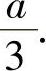
例3.8.5 求二元函数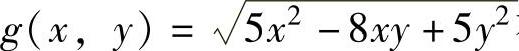 在约束条件x2+y2-xy=75下的最大值.
在约束条件x2+y2-xy=75下的最大值.
精解 本题应使用拉格朗日乘数法求解,但函数g(x,y)的表达式比较复杂,不易求解,所以需对目标函数作些转换.
考虑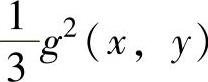 ,并将x2+y2-xy=75代入化简,由此得到的目标函数记为h(x,y),显然在x2+y2-xy=75下g(x,y)与h(x,y)有相同的最大值点.
,并将x2+y2-xy=75代入化简,由此得到的目标函数记为h(x,y),显然在x2+y2-xy=75下g(x,y)与h(x,y)有相同的最大值点.
由于 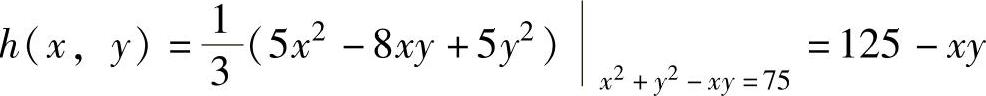 ,所以作拉格朗日函数
,所以作拉格朗日函数
H(x,y)=(125-xy)+λ(x2+y2-xy-75),
则 Hx′=2λx-(1+λ)y,Hy′=2λy-(1+λ)x.于是方程组
式(1)+式(2)得(λ-1)(x+y)=0,即λ=1,x=-y.
当λ=1时,由式(1)得x=y.代入式(3)得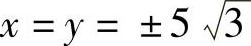 ;当x=-y时,代入式(3)得x=-y=±5.于是在约束条件x2+y2-xy=75下,h(x,y)的可能极值点为
;当x=-y时,代入式(3)得x=-y=±5.于是在约束条件x2+y2-xy=75下,h(x,y)的可能极值点为
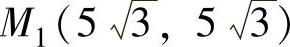 ,
,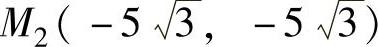 ,M3(5,-5),M4(-5,5).
,M3(5,-5),M4(-5,5).
由于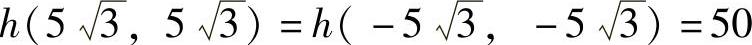 ,h(5,-5)=h(-5,5)=150,所以g(x,y)在约束条件x2+y2-xy=75下的最大值为
,h(5,-5)=h(-5,5)=150,所以g(x,y)在约束条件x2+y2-xy=75下的最大值为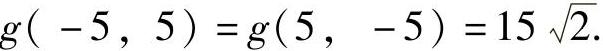
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




