2016考研数学（一）典型题660-多元函数极值计算

【主要内容】

1.二元函数极值的定义设二元函数f（x，y）在点（x₀，y₀）的某个邻域内有定义.如果在此邻域内对任意（x，y）≠（x₀，y₀）都有

f（x，y）<f（x₀，y₀）（或f（x，y）>f（x₀，y₀）），

则称f（x₀，y₀）是f（x，y）的一个极大值（或极小值），称（x₀，y₀）为f（x，y）的极大值点（或极小值点）.极大值与极小值总称极值，极大值点与极小值点总称极值点.

2.二元函数极值存在的必要条件

设二元函数f（x，y）在点（x₀，y₀）处有偏导数，则它在点（x₀，y₀）处取得极值的必要条件为

f_x′（x₀，y₀）=0且f_y′（x₀，y₀）=0（称满足f_x′（x，y）=0且f_y′（x，y）=0的点（x₀，y₀）为f（x，y）的驻点）.

注 函数极值的必要条件可以推广.

设二元函数f（x，y）在点（x₀，y₀）的某个邻域内有定义，则它在点（x₀，y₀）处取得极值的必要条件为

f_x′（x₀，y₀）=0（或不存在）且f_y′（x₀，y₀）=0（或不存在）.

由此可知，对于二元函数f（x，y），它的可能极值点来自三个方面：

（ⅰ）使f_x′（x，y），f_y′（x，y）都为零的点；

（ⅱ）使f_x′（x，y）为零而f_y′（x，y）不存在或者使f_y′（x，y）为零而f_x′（x，y）不存在的点；

（ⅲ）使f_x′（x，y），f_y′（x，y）都不存在的点.

3.二元函数极值的充分条件

设二元函数f（x，y）在点（x₀，y₀）的某个邻域内有二阶连续偏导数且

f_x′（x₀，y₀）=f_y′（x₀，y₀）=0.

记A=f″_xx（x₀，y₀），B=f″_xy（x₀，y₀），C=f″_yy（x₀，y₀），则

（1）当AC-B²>0时，f（x₀，y₀）是f（x，y）的一个极值，且当A>0时，是极小值，当A<0时，是极大值.

（2）当AC-B²<0时，f（x₀，y₀）不是极值.

（3）当AC-B²=0时，f（x₀，y₀）是否为极值需具体讨论（一般通过极值的定义讨论）.

4.二元函数极值的计算步骤

二元函数f（x，y）的极值可按以下步骤计算：

（1）确定f（x，y）的定义域D（设f（x，y）在D上有二阶连续偏导数）；

（2）计算f（x，y）在D上的所有驻点，记为（x₁，y₁），（x₂，y₂），…，（x_n，y_n）；

（3）逐一判断各个驻点是否为极值点，如果是极值点，则同时确定其是极大值点还是极小值点，并求出对应的极大值或极小值.

【典型例题】

例3.7.1 （单项选择题）已知二元函数f（x，y）在点（0，0）的某个邻域内连续，且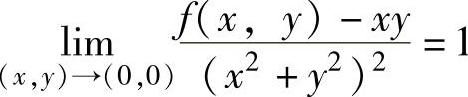，则（ ）.

A.（0，0）不是f（x，y）的极值点

B.（0，0）是f（x，y）的极大值点

C.（0，0）是f（x，y）的极小值点

D.无法判定（0，0）是否为f（x，y）的极值点

精解 可由二元函数极值的定义进行判定.

由题设知，在点（0，0）的充分小邻域内有

f（x，y）=xy+（x²+y²）²+o（（x²+y²）²）.(www.xing528.com)

由此可知，在点（0，0）的充分小邻域内，存在使f（x，y）>0的点，也有使f（x，y）<0的点.所以，（0，0）不是f（x，y）的极值点.

因此本题选A.

例3.7.2 求二元函数z=x⁴+y⁴-x²-2xy-y²的极值.

精解 二元函数在整个xOy平面上有定义，且在其上有二阶连续偏导数，

z_x′=4x³-2x-2y，z_y′=4y³-2x-2y，

A（x，y）=z″_xx=12x²-2，B（x，y）=z″_xy=-2，C（x，y）=z″_yy=12y²-2.

方程组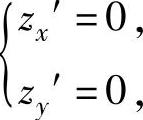即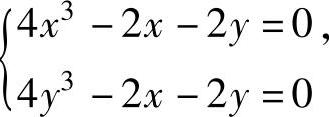的第一个方程减去第二个方程得y=x.将它代入第一个方程得

4x³_-4x=0， 即 x=-1，1，0.

对应地有y=-1，1，0.所以f（x，y）有驻点

（-1，-1），（1，1），（0，0）.

由于A（-1，-1）=10>0，且（AC-B²）|_{（-1，-1）}=96>0，所以z（-1，-1）=-2是极小值.同样z（1，1）=-2也是极小值.

由于（AC-B²）|_（0，0）=0，所以需用其他方法讨论z（0，0）是否为极值.因为z=x⁴+y⁴-（x+y）²，所以在点（0，0）的充分小去心邻域内，当x+y=0时z>0；当x+y≠0时z<0，因此z（0，0）不是极值.

例3.7.3 求二元函数f（x，y）=x²（2+y²）+ylny的极值.

精解 f（x，y）在其定义域y>0上二阶连续可导，且

f_x′（x，y）=2x（2+y²），f_y′（x，y）=2x²y+lny+1，

A（x，y）=f″_xx（x，y）=4+2y²，B=f″_xy=4xy，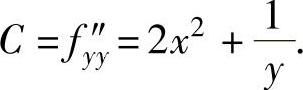

由方程组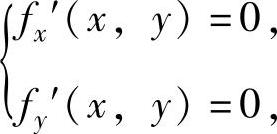 即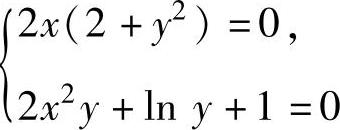

知f（x，y）有唯一驻点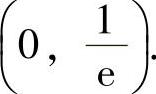

由于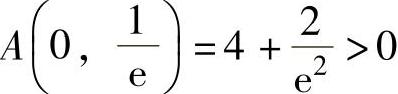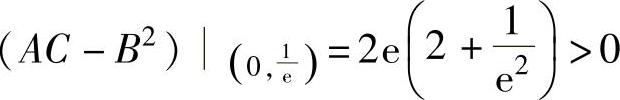，，所以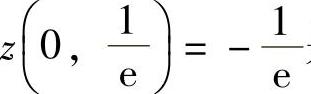是f（x，y）的极小值，f（x，y）无极大值.

例3.7.4 设二元函数z=z（x，y）由方程2x²+y²+z²+2xy-2x-2y-4z+4=0确定，求z=z（x，y）的极值.

精解 本题的z=z（x，y）是二元隐函数，但它的极值的计算方法与二元显函数z=f（x，y）相同.

所给方程两边分别对x，y求偏导数得

由 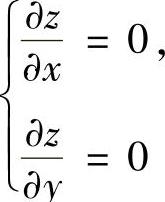即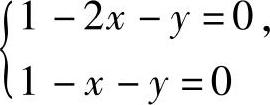得x=0，y=1，对应的函数值为z=1，3.

由式（1）和式（2）得

当x=0，y=1，z=1时，有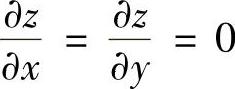且

A（0，1）=2>0，（AC-B²）|_（0，1）=2·1-1²=1>0，

所以z=z（x，y）在点（0，1）处取到极小值z=1.

当x=0，y=1，z=3时，有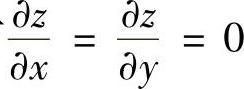，此时

A（0，1）=-2<0，（AC-B²）|_（0，1）=（-2）·（-1）-（-1）²=1>0，

所以z=z（x，y）在点（0，1）处取到极大值z=3.

注 由式（1）和式（2）可知，z=2也可能是z=z（x，y）的极值.由于z=2时，所给方程成为

2x²+y²+2xy-2（x+y）=0，即 x²+（x+y-1）²=1.

由此可知，z=z（x，y）在曲线x²+（x+y-1）²=1上取值为2，从而z=2不可能是z=z（x，y）的极值.