曲面切法计算、曲线切平法线方程

【主要内容】

1.平面方程与空间直线方程

（1）设平面Π通过点（x₀，y₀，z₀），且法向量为（A，B，C）（非零向量），则Π的方程为

A（x-x₀）+B（y-y₀）+C（z-z₀）=0，

或Ax+By+Cz+D=0 （其中D=-Ax₀-By₀-Cz₀）.

注 点（x₀，y₀，z₀）到平面Ax+By+Cz+D=0的距离

（2）设空间直线L通过点（x₀，y₀，z₀），方向向量为（l，m，n）（非零向量），则L的方程为

它的参数方程形式为

注 （ⅰ）由于直线是两个不平行平面的交线，所以直线方程也可以表示为

（ⅱ）点（a，b，c）到直线的距离

（ⅲ）过直线的平面束方程为

λ（A₁x+B₁y+C₁z+D₁）+（A₂x+B₂y+C₂z+D₂）=0，

或 （A₁x+B₁y+C₁z+D₁）+μ（A₂x+B₂y+C₂z+D₂）=0.

2.曲面的切平面与法线方程

（1）曲面方程

曲面方程的一般形式为F（x，y，z）=0.如果任意与z轴平行的直线与该曲面的交点不多于一个，则曲面方程可以表示为z=f（x，y）的形式.

常用曲面有

（ⅰ）旋转曲面

yOz平面上的曲线绕z轴旋转一周而成的旋转曲面方程为

例如，曲线绕z轴旋转一周而成的旋转抛物面方程为z=x²+y².

（ⅱ）柱面

平行于定直线并沿定曲线C移动的直线L形成的曲面称为柱面，其中称C为该柱面的准线，称动直线L为该柱面的母线.例如，以xOy平面上的曲线为准线，平行于z轴的动直线L为母线的柱面方程为f（x，y）=0.

（ⅲ）二次曲面

（a）椭圆锥面：

（b）椭球面： 当a=b=c=R时，椭球面成为球面：（x-x₀）²+（y-y₀）²+（z-z₀）²=R²（点（x₀，y₀，z₀）是球心，R是半径）.

（c）单叶双曲面：

(d)双叶双曲面：

（e）椭圆抛物面：

（f）双曲抛物面：

（2）曲面的切平面方程及法线方程

设点M₀（x₀，y₀，z₀）位于曲面Σ：F（x，y，z）=0上，并且三元函数F（x，y，z）在点M₀处可微，F_x′，F_y′，F_z′在点M₀处不全为零，则称n=（F_x′（x₀，y₀，z₀），F_y′（x₀，y₀，z₀），F_z′（x₀，y₀，z₀））或（-F_x′（x₀，y₀，z₀），-F_y′（x₀，y₀，z₀），-F_z′（x₀，y₀，z₀））为Σ在点M₀处的法向量，此时Σ在点M₀处的切平面方程为

F_x′（x₀，y₀，z₀）（x-x₀）+F_y′（x₀，y₀，z₀）（y-y₀）+F_z′（x₀，y₀，z₀）（z-z₀）=0，法线方程为

3.空间曲线的切线与法平面方程

（1）空间曲线方程

空间曲线Γ是两个曲面F（x，y，z）=0与G（x，y，z）=0的交线，所以它的方程为

空间曲线的参数方程为

（2）空间曲线的切线方程与法平面方程(www.xing528.com)

设点M₀（x₀，y₀，z₀）位于曲线上（对应的参数为t₀），x（t），y（t），z（t）在t=t₀处可微，x′（t₀），y′（t₀），z′（t₀）不全为零，则称τ=（x′（t₀），y′（t₀），z′（t₀））或（-x′（t₀），-y′（t₀），-z′（t₀））为Γ在点M₀处的切向量.此时，Γ在M₀处的切线方程为

法平面方程为

x′（t₀）（x-x₀）+y′（t₀）（y-y₀）+z′（t₀）（z-z₀）=0.

【典型例题】

例3.6.1 设曲线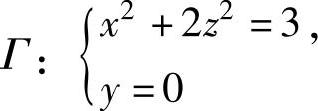绕x轴旋转一周而成的旋转曲面为Σ，求Σ在点（1，0，-1）处的内侧法向量的方向余弦.

精解 先写出Σ的方程，然后计算在点（1，0，-1）处的内侧法向量的方向余弦.

由于Σ是由Γ绕x轴旋转一周而成的旋转曲面，所以Σ的方程为

，即 x²+2y²+2z²-3=0 （椭球面）.

由于点（1，0，-1）位于Σ的下半空间，所以通过此点的内侧法向量与z轴的夹角为锐角，即方向余弦cosγ>0.

记F（x，y，z）=x²+2y²+2z²-3，则

F_x′（1，0，-1）=2x|_x=1=2，

F_y′（1，0，-1）=4y|_y=0=0，

F_z′（1，0，-1）=4z|_z=-1=-4.

所以，Σ在点（1，0，-1）处的法向量为（2，0，-4），从而内侧法向量的方向余弦为

例3.6.2 求曲线在点处的切线方程与法平面方程.

精解 先写出曲线C的参数方程，然后计算C在点处的切线方程和法平面方程.

记x=cost，y=sint，则由x-y+z=2得z=2-cost+sint.于是曲线C的参数方程为

且点对应的参数为由此得到曲线C在点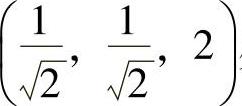处的切向量为

所以曲线C在点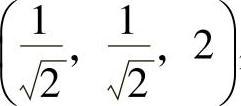处的切平面方程为

，即 ，

法线方程为

例3.6.3 设有曲面S：x²+y²+z²=x，平面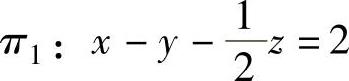和平面π₂：x-y-z=2.求S的切平面π，使π垂直于π₁与π_2.

精解 先算出切平面π的法向量n，然后计算切点（x₀，y₀，z₀）.由此即可算出π的方程.

记π₁，π₂的法向量分别为n₁，n₂，则

所以，由题设知S的切平面的法向量

（由于π垂直于π₁与π₂，所以π的法向量n垂直于n₁，n₂，从而可取n=n₁×n₂）.

设切点为（x₀，y₀，z₀），记F（x，y，z）=x²-x+y²+z²，则S在点（x₀，y₀，z₀）处的法向量为

显然，它的分量与n的分量对应成比例，所以由式（1）与式（2）得

， 即

由于（x₀，y₀，z₀）∈S，即x²₀+y²₀+z²₀=x₀，所以将式（3）代入得

于是有，即切点为

由此可知，所求的切平面π的方程为

和，

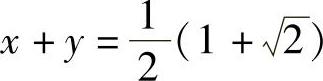即 和

注 向量a=（a₁，a₂，a₃）与b=（b₁，b₂，b₃）的向量积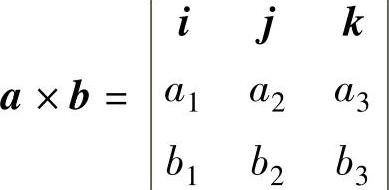，它是既与a又与b垂直的向量.