二元函数方向导数与梯度

【主要内容】

1.二元函数情形

（1）方向导数的定义与计算公式

设l是xOy平面上引自点（x₀，y₀）的射线，它的方向余弦为cosα，sinα（其中α为l与x轴正向的夹角）.于是l上任一点（x，y）的坐标可表示为x=x₀+rcosα，y=y₀+rsinα，其中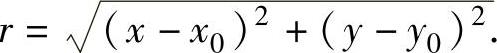又设二元函数f（x，y）在点（x₀，y₀）的某个邻域内有定义，如果极限

存在，则称这个极限值为f（x，y）在点（x₀，y₀）处沿l方向的方向导数，记为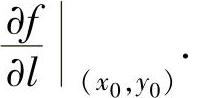f（x，y）在点（x，y）处沿l方向的方向导数记为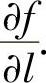

如果函数f（x，y）在点（x，y）处可微，则f（x，y）在该点处沿任意方向l的方向导数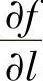都存在，且

（2）梯度的定义

设二元函数f（x，y）在点（x₀，y₀）处可微且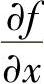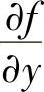，不全为零，则称向量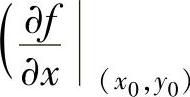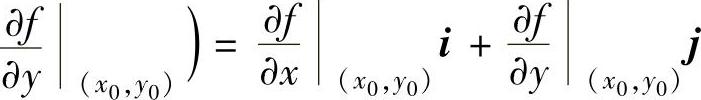，为f（x，y）在点（x₀，y₀）处的梯度，记为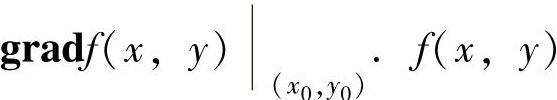在点（x，y）处的梯度记为gradf（x，y）.

由于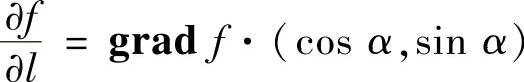，所以函数f（x，y）在点（x，y）处的方向导数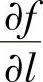沿梯度gradf（x，y）取得最大值|gradf（x，y）|.

注 向量a=（a₁，a₂）与b=（b₁，b₂）的数量积为a·b=a₁b₁+a₂b₂.

2.三元函数情形

（1）方向导数的定义与计算公式

设l是Oxyz空间上引自点（x₀，y₀，z₀）的射线，它的方向余弦为cosα，cosβ，cosγ（其中α，β，γ分别为l与x轴、y轴与z轴正向的夹角）.于是l上的任一点（x，y，z）的坐标可表示为x=x₀+rcosα，y=y₀+rcosβ，z=y₀+rcosγ，其中r=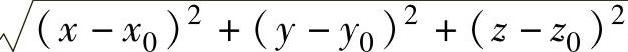.又设三元函数f（x，y，z）在点（x₀，y₀，z₀）的某个邻域内有定义，如果极限

存在，则称这个极限值为f（x，y，z）在点（x₀，y₀，z₀）处沿l方向的方向导数，记为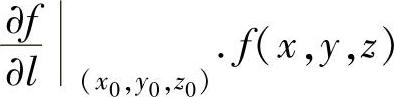在点（x，y，z）处沿l方向的方向导数记为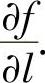

如果函数f（x，y，z）在点（x，y，z）处可微，则f（x，y，z）在该点处沿任意方向l的方向导数都存在，且

其中，cosα，cosβ，cosγ是l的方向余弦.

（2）梯度的定义(https://www.xing528.com)

设三元函数f（x，y，z）在点（x₀，y₀，z₀）处可微且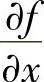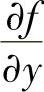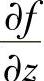，，不全为零，则称向量

为f（x，y，z）在点（x₀，y₀，z₀）处的梯度，记为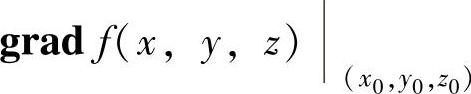，f（x，y，z）在点（x，y，z）处的梯度记为gradf（x，y，z）.

由于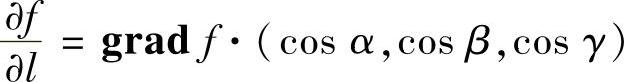，所以函数f（x，y，z）在点（x，y，z）处的方向导数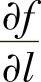沿梯度gradf（x，y，z）取得最大值|gradf（x，y，z）|.

注 向量a=（a₁，a₂，a₃）与b=（b₁，b₂，b₃）的数量积a·b=a₁b₁+a₂b₂+a₃b₃.

【典型例题】

例3.5.1 设三元函数f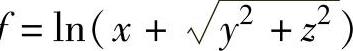，求该函数在点A（1，0，1）处沿点A指向点B（3，-2，2）方向的方向导数.

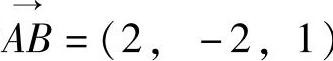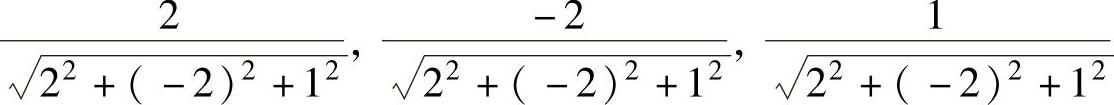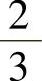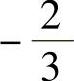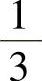精解 由于方向l即为的方向，所以l的方向余弦cosα，cosβ，cosγ为，即，，，从而，

例3.5.2 设三元函数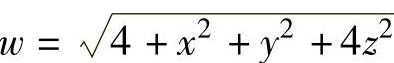，求过点M（1，1，1）且与方向l垂直的平面方程，其中l是使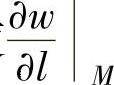为最大的方向.

精解 因为使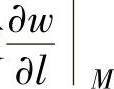为最大的方向是

它即为所求平面的法向量，因此所求的平面方程为

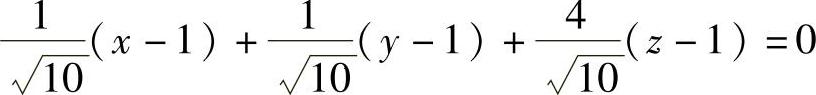，即 x+y+4z=6.

注 平面方程的一般形式为Ax+By+Cz+D=0，其中（A，B，C）是它的法向量.过点（x₀，y₀，z₀），且法向量为（A，B，C）的平面方程可写成A（x-x₀）+B（y-y₀）+C（z-z₀）=0.

例3.5.3 设二元函数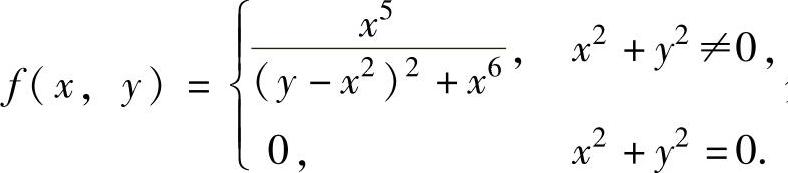分别计算使方向导数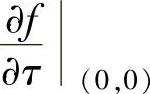（其中τ的方向余弦为cosα，sinα，α∈[0，2π））为最大和最小时的α.

精解 先由定义计算方向导数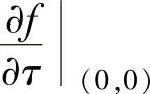，然后确定使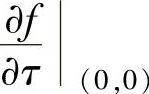为最大和最小的α.

由于

所以，使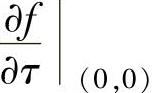为最大和最小的α分别为0和π.