短文本表示建模与应用：随机梯度算法

为了训练模型，本书需要解决式的优化问题。一种常用的方法是使用基于梯度的方法：反复地计算训练集上的损失L（·）的估计和参数集合Λ关于损失估计的梯度值，并将参数值向与梯度相反的方向调整。不同的随机梯度方法的主要区别在于如何对损失进行估计，以及如何定义“向与梯度相反的方向调整参数值”。

对于寻找最小化函数y=f（x）的标量值x的任务，常规思路是计算该函数的二阶导数，解得到极值点。这种思路在多变量函数中的可行性较低，因此一种替代思路是采用数值法：计算一阶导数f ′（x），然后以一个初始猜测值x开始，求值∇=f ′（x）就会给出调整的方向。如果∇=0，那么x就是极值点（即最优选择）；否则，通过令x′←x−ε·∇向与∇相反的方向调整x，其中ε 表示学习率。如果ε的取值足够小，则f′（x）会小于f（x）。重复上述过程（同时适当地对学习率ε进行衰减）就能找到一个极值点。如果函数f（·）是凸函数，则该最优值是全局最优的；否则，上述过程仅能找到局部最优值。下文以随机梯度下降算法为例来介绍随机梯度算法的原理。

随机梯度下降算法及其变形是训练线性模型的有效且通用的方法。该算法首先接收一个被Λ参数化的函数f（·）、一个目标函数L（·）以及期望的输出对{〈xi，yi|〉i=1，2，…，m}；然后，尝试设定参数，使得在训练样例上的累计损失足够小。随机梯度下降算法的流程如下：

第1步，采样一个训练样本〈xi，yi〉，计算损失函数ℓ（f（xi；Λ），yi）。

第2步，计算ℓ（f（xi；Λ），yi）关于Λ的梯度，记为∇。

第3步，Λ ←Λ−ε·∇。

第4步，如果不满足终止条件，则转到第1步。

随机梯度下降算法的目的是设定参数Λ，以最小化训练集上的总体损失，即。算法的工作方式是反复随机抽取一个训练样例，计算这个样例上的误差关于参数Λ的梯度。假设输入和期望输出是固定的，损失被认为是一个关于参数Λ的函数。然后，参数Λ被以与梯度相反的方向进行更新，比例系数为学习率ε（学习率在训练过程中是可以不变的，但也可以基于时间步衰减）。

需要注意的是，随机梯度下降算法第1步所计算的误差是基于一个训练样例的，因此仅仅是对需要最小化的全局损失ℓ（·）的大致估计。损失计算中的噪声可能导致不准确的梯度。减少这种噪声的常见方法是在m′个样例上估计损失和梯度，因此小批量（Mini-Batch）随机梯度下降算法应运而生，该算法的流程如下：

第1步，采样包含个训练样本的一个小批量样例{〈xi，yi|〉i=1，2，…，m′}，i←1，∇′←0。(www.xing528.com)

第2步，计算损失函数ℓ（f（xi；Λ），yi）。

第3步，计算ℓ（f（xi；Λ），yi）关于Λ的梯度，记为∇。

第4步，。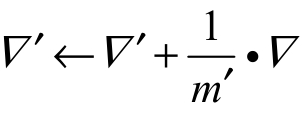

第5步，i ←i+1，如果i ≤m′，就转到第2步，否则转到第6步。

第6步，Λ ←Λ−ε·∇′。

第7步，如果不满足终止条件，就转到第1步。

小批量随机梯度下降算法的第2步～第5步估计了基于小批量样例的总体损失的梯度。循环之后，∇′包含了梯度估计，参数Λ被朝向∇′更新。批量的规模大小m′在[1，]m范围内，相关研究已经证明：较大的批量规模m′能够提供对于总体梯度的更好估计，而较小的批量规模m′能够收到更快的收敛速度。除了提升梯度估计的准确性外，小批量随机梯度下降算法也能够有效提高训练效率。针对适当的m′，一些计算体系（如GPU等）可以基于第2步～第5步进行高效的并行计算法方式。

随机梯度下降算法既可以用于优化凸函数，也可以用于优化非凸函数。当被优化的对象是凸函数时，带有适当递减的学习率的随机梯度下降算法能够保证收敛到全局最优解。这是因为，凸函数是二阶导数总是非负的函数，所以这一性质可保证凸函数有一个最小值点。凸函数具有这种使用基于梯度的最优化方法即可最小化的性质，仅沿着梯度即可到达极值点，一旦到达极值点就能够得到全局极值点。当被优化的对象是非凸函数时，不能保证找到全局最优价。这是因为，非凸函数是二阶导数总是负或者0的函数，因而存在一个最大值点。所以，对于非凸函数，基于梯度的最优化算法可能到达局部极值点而无法找到全局极值点。