平方米的图形面积最大

从几何学角度上讲，等周长的正多边形的边数越多，它的面积就越大，圆形的面积为最大。如果帕霍姆圈地时跑出一个周长为40俄里的圆，那么他圈出的土地面积为≈127平方俄里。

等周长的任何图形中，没有哪个图形的面积大于圆的面积。

这就是圆形的特性：等周长的情况下，圆比任何一种形状的图形的面积都大。可能你会问这是如何证明出来的，我们可以给予证明，但这些数据并不严谨——这是数学家施泰纳在证明特性时提出来的。他的论证很烦琐，如果你对此不感兴趣，可以跳过这段内容，当然了，也不会影响到你对后面知识的学习。

要证明在等周长的图形中，圆形的面积最大。首先要知道这个图形是凸边的。也就是说，这个图形的任意一条弦都在图形之内。如图12-4所示，这是既定图形AaBC，它有一条弦AB在图形外，我们可以用和它相对称的b弧代替a弧。这时图形AbBC的周长没有改变，面积却增加了。也就是说，在周长相等的情况下，类似AaBC的图形绝不可能成为在相等周长情形下有最大面积的图形。

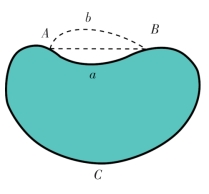
图12-4 面积最大的图形应该是凸边图形

那么具有最大面积的图形就是凸边图形。这个图形还有一个特性：任意一条把图形周长一分为二的弦，也能把图形的面积一分为二。如图12-5所示，假设图形AMBN就是我们要求解的图形，弦MN能把它的周长分为相等的两份。那么我们就需要证明AMN和MBN的面积是相等的。如果一部分比另一部分大，就是AMN＞MBN，那么把图形AMN沿着MN线对折，就得到了图形AMA′N它的周长和原来相等，但面积却比AMBN大。也就是说，AMBN里的弦把它的周长分为两等份，却把面积分为两个不相等的部分。那这个图形AMBN就不是我们要想的图形（等周长的图形中，它不可能是最大面积的图形）。

图12-5 面积最大的图形应该是凸边图形

在这里，还要证明一个定理：所有已知两条边长的三角形中，两条边的夹角是直角的三角形的面积最大。

要证明这一点，可以回忆曾求过已知a、b两边和两边之间的夹角C的三角形面积S的三角形公式：(www.xing528.com)

显然，两条边既定的情况下，sinC等于1时是最大数值，这时这个公式的值也最大。如果正弦值为1，就说明这个角是直角，我们要证明的就是这个问题。

现在我们就来证明在所有周长相等的图形中，圆形的面积最大。要证明这一点，可以假设面积最大的非圆形凸边图形MANBM存在（图12-6）。在这个图形中，我们作一条平分周长的弦MN，这条弦还可以把图形的面积平分。将图形的一半MKN沿着MN线对折，使它与原来的位置（MK′N）对称。图形MNK′M的周长和面积与原来的图形MKNM的周长和面积相等。因为MKN弧不是一个半圆周（所以才需要证明），所以这条弧上有一些点，它们M、N的连线无法构成直角。如果K为其中一点，K′是和它对称的一点，就是说，角K和角K′都不是直角。保持MK、KN、MK′和NK′边的长度不变时移动它们的位置，可以使它们之间的夹角K、K′成为直角，这就得到了全等三角形。如图12-7所示，用弦把这两个三角表并在一起，把有阴影的部分连接到相应的位置。就有了和原图形同长相同的图形M′KN′K′M′，但它的面积要比原图形大（因为直角三角形M′KN′和M′K′N′的面积要大于三角形MKN和MK′N的面积）。也就是说，等周长的非圆形的图形的面积不可能是最大的。我们不可能做出等周长的比圆形面积更大的图形来。

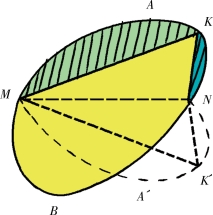
图12-6 假设的确有面积最大的非圆形的凸边图形存在

图12-7 证明等周长的图形中，面积最大的图形是圆形

这就是证明在等周长的矩形中，圆形面积最大。

想要证明这一论点是正确的也不难：面积相同的图形中，圆形的周长是最短的。这个问题在介绍正方形的特性一节中已经做过论证了。