题:如图10-15所示,把五个图形画在一张纸上。再用铅笔把它们描出来,笔不能中断,每一笔都不可以有重复。
很多人都会从第四个图形d开始描,因为他们认为这个图形是最简单的,但却都没能把这个图形一笔画下来。可前两个图形反而轻轻松松地就画下来了,甚至连看起来非常复杂的第三个图形也画了出来,只是第五个图形和第四个一样,没人一笔就画得下来。
为什么有的图形可以一笔画出,有的就不行呢?是因为我们没有创造力,还是有的图形本身就不具备一笔画出的条件?能不能根据图形的一些特性而判断出它们能不能一笔画成呢?
解:图形线会合的每个交点被称为“交点”,如果在交点会合的线条数为偶数,这个点就是偶交点,如果这个线条数为奇数,那么这个点就叫奇交点。图形a上的所有交点都是偶交点,图形b上有A、B两个奇交点。图形c上,横穿过几个图形的线段两端是奇交点。图形d和e上分别有四个奇交点。
先看所有交点都是偶交点的图形,如图形a,我们从任意点S开始画起,比如说在经过A交点时会画出通往和离开A点的两条线。因为出入每一个偶交点的线条数相同,所以我们每次从一个交点移到另一个交点,就会减少两条没有画到的线条。所以把所有的线条画了一遍后,就会回到起点S。
但如果回到起点后就没有出路了,而图形上还有一条线条没有被描过,它来自B点,而我们已经到过B点了。也就是说我们要改路线:到达B点后,要先把漏画的线条画上,再回到B点,按原路前进。
假设以这样的方法描画图形a:先沿着三角形ACE的边开始画,再回到A点,沿着圆周ABCDEFA(图10-15a)画。这时,只有三角形BDF没有画,所以这时要先画完三角形BDF,再离开B交点画弧线BC。
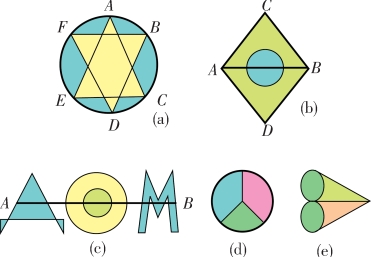
图10-15 请把这几个图形一笔画出,中间不能停笔,每一笔不得重复
也就是说,如果一个图形的所有交点都是偶交点,那么从它的任意一点出发都可以一笔画成整个图形,并且完成时的终点和起点相同。
再来看有两个奇交点的图形:
比如说图形b有A、B两个奇交点。
这样的图形也可以一笔画就。(https://www.xing528.com)
其实从第一个奇交点开始画,沿着随便哪条线到第二个奇交点,比如在图10-15b,从A点开始,沿着ACB线画到B。
描完这条线后,奇交点中就少了一条线,就像图形里从来没有这条线一样。然后两个奇交点就成了偶交点,由于图形里没有其他的奇交点,只有偶交点了。比如图形b中,描完ACB,就只有一个三角形和圆形了。
根据前文的介绍,这样的图形是可以一笔画就的,那么整个图形也是可以的。
但要注意的是,从第一个奇交点为起点,选择通向第二个奇交点的路线不要形成和给定的图形隔离的图形[2]。如图10-15中的图形b,如果沿着直线AB从奇交点A描到奇交点B,是注定会失败的,因为圆周被图形的剩余部分隔开了,根本没办法描到。
如果一个图形有两个奇交点,那么最好的方法应该是从其中一个奇交点为起点描至另一个奇交点,两个点不重合。
由此得出,如果一个图形有四个奇交点,那么是不可能一笔画就的,要用两笔才可以,这就不合题意了。比如图10-15的图形d和e就是这样的情况。
是的,只要我们能够正确思考,就能不必浪费时间和精力就预见很多情况,几何学在这个时候就帮了我们大忙了。
可能我们在这里研究的问题让你感到疲惫,但你会得到回报,那就是在你做类似题目时几何学会派上用场。
你总是能预先知道:给定的图形是否可以一笔画就,还知道应该从哪个点出发。
现在,你可以为你身边的人出图10-16的图形考考他们,看他们能不能一笔画出。
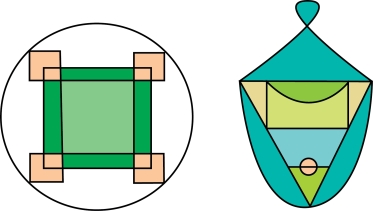
图10-16 一笔可以画就的两个图形
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




