【摘要】:假设OabcA为台球被击打后的路径。由图中的三角形全等关系,可以得出ab1=ab,b1c1=bc,c1A1=cA,也就是说,直线段OA1与折线段OabcA长度相等。所以,当你向想象中的A1点击球时,台球就会沿着OabcA滚动,接着台球就会落入A袋中。图10-11 想象三张同样的球桌并排放置,你向最远的球袋击球
打台球的时候,如果你想通过撞击一边、两边或三边的台边使球进入袋中,而不是直接击打台球使它进入袋中,就要快速地在头脑中作图,解答一道几何题。
首先要用目测法找到台球第一次撞台边的点位。在一个质量上乘的台球桌案上,反弹定律就决定了台球的路径(入射角等于反射角)。
题:要使在球案中央的台球撞击三边反弹落入A袋中(图10-10),那么要找到台球的方向需要用到哪些几何知识的帮助呢?
图10-10 台球桌上的几何学
解:想象这样的场景,在你的球台旁边,还有三张同样的球台并排放着,你把球对着想象中的第三张球台距离你最远的那个球袋打过去。
如图10-11所示,可以看出这点。假设OabcA为台球被击打后的路径。如果围绕着CD把台球桌ABCD翻转180°,它就会到图片的中位置Ⅰ,然后围绕着AD线再翻转一次球桌,再围绕着BC线翻转一次,那么台球桌这时的位置就是图中Ⅲ的位置。这时的A袋就在A1的点位。(https://www.xing528.com)
由图中的三角形全等关系,可以得出ab1=ab,b1c1=bc,c1A1=cA,也就是说,直线段OA1与折线段OabcA长度相等。
所以,当你向想象中的A1点击球时,台球就会沿着OabcA滚动,接着台球就会落入A袋中。还要考虑一下,在什么样的情况下,直角三角形A1EO的OE和A1E两边会相等?

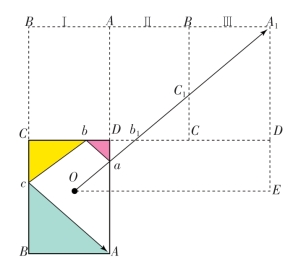
图10-11 想象三张同样的球桌并排放置,你向最远的球袋击球
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




