一些模型的设计和制造者，还有一些无线电爱好者都喜欢亲手制作模型，经常会在操作过程中遇到难题。
题：找一块铁片，在上边剪出一个指定边数的正多边形。
这道题的意思可以这样理解：
把一个圆周n等分，n是整数。
解：我们先不用量角器解题，想想怎样用圆规和直尺的几何学知识解题。
首先想一想用圆规和直尺能把一个圆周几等分？这个问题早就有了答案：不可为任何数的等分。
可为：2，3，4，5，6，8，10，12，15，16，17，… …，257，… …等分。
不能为：7，9，11，13，14，… …等分。
还有一个问题就是没有统一的作图方法，比如说我们要把一个圆周15等分和12等分的方法不一样，方法也很多。
这就需要一种几何学的方法，即使只能求出近似值也可以，但一定要是能把一个圆周分成任意份的方法，且通用简便。
但几何学教科书的编者们还没有注意这个问题，我们在这里就介绍一种求解这类题目的简便有趣的方法。
如图10-9所示，要把一个圆周分为九等份。AB为圆的任意直径，以AB为边作一个等边三角形ACB，在D点把直径AB分为AD和DB两段，并使它们的比例为AD∶AB＝2∶9（若要将圆周等分为几份，则AD∶AB＝2∶n）。(www.xing528.com)
图10-9 把圆周n等分的近似值的作法
连接C、D两点，并延长至和圆周相交点E处。这样弧线AE就是圆周的九分之一（或AE＝
也就是说，弦AE是这个圆的内接正九边形（或n边形）的一条边。这个数值的误差只有0.8%。
要把用上述作图方法作出的圆心角AOE和划分的等分n数之间的关系式表示出来就是这样一个公式：
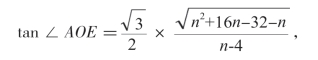
如果n较大，用上述公式也可以计算出：
另外，把圆周n等分时，圆心AOE是
。把
与计算得出的∠AOE的角度相比较就会发现用上述方法计算出现的误差。
下面是和等分数目n值有关的数值。
从这个表中可以看出，用上述方法把一个圆周分为5、7、8、10等分时，误差不算太大，只是0.07%～1%，这样的误差在大多数实际操作中都是允许的。但n的增加就使这种方法的误差越来越明显，但据实际研究，n为任何数目时，误差都不会超过10%。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
