拿破仑数学题：如何把圆O四等分？

上述题目中，在图纸上事先给出一个圆周的条件下，我们没用圆规，只利用直尺就完成了作图。再来看一道与之相反的题目：不许使用直尺，只能使用圆规作图。拿破仑很热爱数学，这是众所周知的事，这道题引起了他极大的兴趣。意大利学者马克罗尼有一部著作介绍了这类作图法，拿破仑阅读后，给法国数学家出了这样一道题。

题：已知圆心的位置，请不用直尺把这个圆四等分。

解：如图10-5所示，要把圆O四等分。首先取圆周上的任意一点A，从A点沿着圆周以圆O的半径为半径画三次半径，就得到了B、C和D点。这时你就知道弧线AC占圆周长的弦AC也是内接等边三角形的一边，等于r，r为圆的半径，AD则为圆周的直径，以AC为半径，从A点和D点作相交于M点的弧。我们要证明的是，MO间的距离是圆周的内接正方形的边长。三角形AMO的直角边：

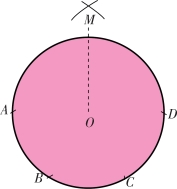
图10-5 只使用圆规如何把一个圆周四等分

(www.xing528.com)

这就是圆的内接正方形的边长，然后把圆规的开度摆成与MO相等的长度，在圆周上划出四个点，这四个点就是这个圆的内接正方形的四个顶点，也就把这个圆四等分了。

题：如图10-6所示，要求把A和B之间的距离增大五倍或指定的倍数，但不能使用直尺。

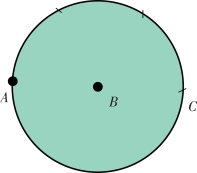
图10-6 只用圆规如何把AB间距扩大n倍（n为整数）

解：以B点为圆心，以AB长为半径画一个圆。从A点在圆周上三次画出AB的距离；从而得到C点，那么C点和A点同在一条直径上，AC为AB距离的两倍，以点C为圆心，以BC为半径画一个圆，用上述方法找到这个圆上与点B相对的点，这个点离点A的距离超过AB的距离的3倍，以下依此法类推。