格罗列夫创造两项世界纪录：北极飞行+趣味几何学

你应该还记得苏联英雄格罗莫夫和他的朋友们从莫斯科成功地飞越北极抵达美国的圣贾辛托的壮举。格罗列夫在长达62小时17分钟的飞行时间里创造了不着陆直线飞行10 200千米和不着陆折线飞行11 500千米的两项世界纪录。

经常有人这样问，这些飞越北极的英雄们的飞机会和地球一起绕着地轴旋转吗？却很少有人能给出正确的答案。任何飞机都是随着地球旋转的。因为飞机飞上高空后，只是离开了地球表面，却并没有脱离大气层，依旧受着地心引力的作用，围绕着地轴作旋转运动。

一架飞机，从莫斯科越过北极到达美国，它与地球一起绕着地轴旋转的轨迹是什么样的？

确切一点，应该说“一个物体运动”时，是指这个物体相对于另一个物体的位移。所以在讨论关于轨迹或运动的问题时，如果没有指明（或没有意识到）数学上的坐标系，也就是说，没有指明物体运动是相对于什么物体发生的，那么这个题目就没有任何意义。

格罗莫夫驾驶的飞机和地球相比，应该算是沿着莫斯科子午线飞行的。和其他子午线一样，莫斯科子午线也是和地球一起绕地轴旋转的。沿着子午线路线飞行的飞机自身也会有旋转，只是这样的运动地面上的观测者是看不出来的。因为它的旋转并不是相对于地球的，而是相对于其他物体在旋转。

这道题看起来很难，我们可以把它简化一下。我们把地球北极周围的区域想象成平铺在和地轴垂直的平面上的一个扁平的圆盘。假设这个平面就是那个“物体”，也就是说，圆盘相对于它绕着地轴旋转；再假设一辆玩具车沿着圆盘的直径之一匀速行驶：把玩具车比作沿子午线飞越北极的飞机。

那么玩具车在我们这个平面上的路径是什么样的呢？

有下面三种情况，我们来分析一下：

1.12个小时之内，玩具车跑完全程；

2.24个小时内，玩具车跑完全程；

3.玩具车在48小时内跑完这段路程。但不管是哪种情况，这个圆盘都会在24小时内旋转一整圈。

如图9-13所示，这是第一种情况。玩具车在12个小时内跑完全程。在这段时间里，圆盘只转动了半周，就是180°，然后A和A′互换位置。在图9-14上，把圆盘的直径分为八等份，玩具车每跑完其中一份区域时要用＝1.5小时。那么玩具车行驶1.5小时后位于什么位置？如果圆盘不旋转，那么玩具车从A点离开，行驶1.5小时到达b点。但圆盘是旋转的状态，1.5小时内，它会转＝22.5°。这时圆盘的b点到了b′点。站在圆盘上并和圆盘一起旋转观测者并不会发现它在转动，只会看到玩具车从A点移到了b点。但不和圆盘一起旋转的人会看到：玩具车沿着曲线从A点到b′点。1.5小时后，玩具车就会出现在c′点。接着，玩具车在接下来的1.5小时会沿着弧线c′d′移动，再过1.5小时，玩具车就会到达中心e点处。

不随圆盘旋转的观测者可能会看到让人惊奇的情景：玩具车会画出一条曲线ef ′g′h′A，而且玩具车最终是停在了起点，而不像人们想象的那样停在直径对面的一点上。

这个现象的原理非常简单：玩具车在后6个小时的行驶过程中，这段半径已经随着圆盘转动了180°，这样，直径前半段的位置就被占据了。甚至在玩具车驶过圆盘中心时仍然随着圆盘一起旋转。在玩具车与圆盘的中心重合时，只是它的一个点而已，玩具车和圆盘在某个时刻都在围绕着这个点旋转。飞机飞过北极上空时也和玩具车和圆盘的情况一样。玩具车沿着圆盘直径一端到另一端的路径，身处不同位置的观测者观测时的样子也是不同的。与圆盘一同旋转的人会认为这段路程是一条直线。但没有与圆盘一同旋转的人则是看到玩具车沿着一条形状很像人的心脏的曲线运动（图9-13）。

假设我们每个人都从地球的核心观察一架飞机，它相对于和地轴垂直的平面飞行，同时假想地球是透明的，你站在地平面上，但不参与地球的旋转，这架飞机穿越北极需要12个小时，在这种情况下，你看到的曲线就如图9-13所示。

图9-13

这里有个实例，把两种运动合二为一：从莫斯科穿越北极到同一纬度正相反的一点的飞行持续时间不是12小时，想要解答这个题目，要先分析下面这个同类题目。

如图9-14所示，这是第二种情况，玩具车用24小时跑完全程。在这段时间内，圆盘转动了一周，观测者对于圆盘来说是静止不动的，他们看玩具车的行程路线时就是图9-14所示的曲线形状。

(www.xing528.com)

图9-14

一个同时参与两种运动的点在静止的平面上的曲线示意图

如图9-15所示，这是第三种情况：圆盘仍然是在24个小时转动一周，但玩具车要用48小时才能从直径的一端到另一端。

这次玩具车行驶完直径路程的需要用小时，也就是6个小时。

在圆盘转动的6个小时内，一共转动了四分之一周，就是90°。所以，玩具车出发6个小时后，它本来应该沿着直径移动到b点（图9-15），但在圆盘旋转之下，这个点就移动到了b′点。6小时后，玩具车会到g点，再接下来的6小时也按之前的规律。就这样，玩具车在48小时内跑完了直径全程，而圆盘转动两整圈，这时的状态是两种运动合二为一了。这使得相对静止的观测者看到了图9-15中的曲线。

图9-15 两种运动合成的曲线

我们现在研究的情形让我们越来越接近飞机穿越北极飞行的实际情况。格罗莫夫用24小时左右的时间从莫斯科飞到北极；这时的观测者身处地球中心，他们看到的轨迹形状就像图9-16所示的前半段相同。格罗莫夫的第二段飞行，持续的时间超过了第一段的50%，另外，北极和圣贾辛托的距离也比莫斯科和北极的距离长50%。所以观测者在静止不动的情况下，就会感觉第二段路程的轨迹形状和第一段路程的路径形状相比，除了长出了50%之外，没有什么不同。

如图9-16所示，这才是最终的曲线。

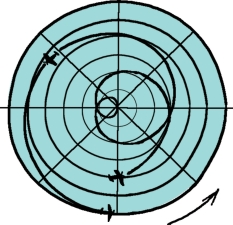
图9-16 没有参与飞行和旋转的观测者想象中的莫斯科——圣贾辛托的飞行路线

也许你会觉得奇怪，为什么从图上看飞行的起点和终点距离这么近呢？

图中所示的莫斯科和圣贾辛托的位置不是同一时刻的，是相隔2.5个昼夜的图。这个问题是不容忽视的。

如果可以从地球的中央观察格罗莫夫穿越北极的飞行，这个形状应该就是图中这样的。这个复杂的旋涡图，我们可以称之为相对的路径，也就是飞机穿越北极飞行的“实际路径”。即使不是这样的情况，它们的运动也是相对的：相对于一个不和地球一起绕地轴旋转的物体来说就像飞机轨道总是相对旋转的地球表面一样。

观察飞机飞行时，如果可以从月球或太阳^[8]上观测的话，那么飞机飞行的轨迹就可能完全变样了。

虽然月球相对地球没有昼夜的旋转，但它却在围着地球旋转，周期为一个月。月球在飞机从莫斯科到圣贾辛托的62小时的飞行中，绕着地球行走了30°的弧线，这就给月球上的观测者观察飞行轨迹时带来了影响。还有第三个运动——在太阳上观测飞机飞行轨迹形状时会受到地球围绕太阳旋转的影响。

恩格斯在《自然辩证法》中这样说：“运动都是相对的，没有单个物体的运动。”

研究过上述题目，我们对恩格斯的这句话深信不疑了。