一个圆沿着同一平面上的一条直线滚动,这个圆上的点都会在这个平面上留下自己的足迹。
如图9-8、图9-9所示,这是一个圆沿着直线或圆滚过后各点的轨迹,仔细观察会发现一条不同的曲线。

图9-8 圆滚线—— 一个圆沿着直线滚过圆周上的A点的轨迹
问题出现了:如图9-9所示,一个圆沿着另一个圆的圆周内边滚动,圆上的一个点在滚动过程中出现的能不能不是曲线的轨迹,而是直线的轨迹?也许你会认为这是不可能的。
我见过一个玩具——走钢丝的女孩,利用的就是这样的设计。这个玩具的制作过程非常简单。找一块厚纸板或厚木板,在上边画一个直径为30厘米的圆,画出它的直径,并把直径线两边延长,在纸板上留下一块空白处。
找到直径的延长线两端,在两端处各插一根针,用一根线穿过针眼,把线水平拉直,把线的两端分别固定在纸板上。然后把纸板上的圆切割下来,用硬纸板切割一个直径为15厘米的圆,把这个圆放进刚切好的大圆孔中。在这个小圆形的边上也插上一根针(图9-10),用硬纸板剪一个走钢丝的女孩,用蜡把女孩的脚固定在这根针上。
图9-10 “走钢丝的女孩”在滚动的圆上沿直线移动的点
把小圆紧贴着大圆孔的边缘滚动,针头和女孩都会沿着细线轻轻地前后滑动。
这个原因很简单,就是因为固定着针的小滚动圆形上的那个点,是沿着圆孔的直径移动的。
如图9-9所示,滚动圆上的点画出的为什么是曲线而不是直线呢?问题的关键就在大圆和小圆直径的比值上。
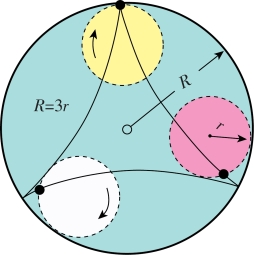
图9-9 三角内圆滚线—— 一个小圆沿着一个大圆的内边滚动,小圆的圆周上一点走过的轨迹,其中R=3r
 (https://www.xing528.com)
(https://www.xing528.com)
图9-11 “走钢丝的女孩”几何示意图
题:证明,一个小圆在一个大圆周里沿着大圆的内边滚动,小圆的直径比大圆的直径小一半,在移动的时候,小圆上任意一点都会沿着大圆的直径方向作直线运动。
解:如图9-12所示,小圆O1的直径比大圆O的直径小一半,那么小圆O1滚动的每一刻,总会有一点在大圆O的圆心处。
看图中小圆O1的A点移动轨迹。
假设小圆O1是沿着AC弧线滚动。
那么A点在小圆O1中的新位置在哪里?
小圆在大圆中是滚动的,而不是滑动的。为了使弧线AC和BC相等,则A点应处在B点处。假设OA=R,∠AOC=a,则AC=R×a;所以BC=R×a,因为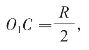 则:
则:
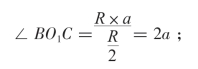
∠BOC=![]() =a,B点仍在OA线上。
=a,B点仍在OA线上。
“走钢丝的女孩”这个小玩具其实就是一个把旋转运动变成直线运动的装置,并不复杂。
自从俄国工业学家波尔祖诺夫发明了第一台热力发动机后,机械师们就迷恋上了这类设计,装置是通过铰链把直线运动传送到某一点的(图9-12)。
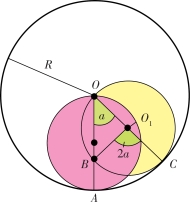
图9-12 “走钢丝的女孩”的几何图解
俄国数学家切比雪夫(1821-1894)是一个天才,他为机械数学理论的发展作出了杰出的贡献。他不只是一位数学家,还是一位优秀的机械师。他研制出了“跖行”机器模型(仍保存在俄罗斯科学院),自行滑动椅装置,还有当时非常先进的算术计算器,等等。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




