我们看到，阿拉伯数学家穆罕默德·本·木兹在自己的著作《代数学》中这样说：
最简便快捷的方法就是把直径乘以3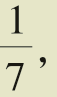
没有其他更好的办法了。
现在的人都知道，阿基米德的
并不能准确表达圆周长和直径的关系，其实这个比值是无法用一个精确的分数表示出来的，即使写出了一个比值，那也只是近似的比值，对于我们日常生活需求来说，它已经足够精确了。16世纪荷兰数学家卢多尔夫在荷兰的莱顿市耐心地把π的值计算到小数后35位，临死前，他还立下遗嘱，要求把他计算出来的这个π值刻在他的墓碑上[1]（图9-1）。他计算出来的π值为：
图9-1 数学家卢多尔夫的墓志铭(www.xing528.com)
3.141 592 653 589 793 238 462 643 383 279 502 88…
1873年，德国的圣克斯把π值计算到了小数点后707位，但这样精确的π值没有实际价值，虽然这样，但有的人还是在往后计算π值，无非是想破圣克斯的“纪录”：1946—1947年，曼彻斯特大学的弗格森和华盛顿的伦奇分别把π值计算到小数点后808位，并且发现圣克斯计算的π值的528位以后是错误的。
假设地球的直径是一个精确的长度，我们要计算地球赤道长度精确到厘米时，在计算的时候只要取π值小数点后的9位即可，如果我们取了π值小数点后的18位，那么我们就可以计算以地球到太阳的距离为半径的圆周长度了，而且这样计算出来的误差非常小，在0.000 1毫米之下（比一根头发的百分之一还要细）。数学家格拉韦清楚地证实了一点，那就是把π值精确到小数点后一百位就已经毫无意义了。他设想有这样一个球体，它的半径是从地球到天狼星的距离，就是等于在132后面再加十个零的千米数：132×1010千米。把这个球体中每一立方毫米中充满100亿个（1010）微生物，然后把这些微生物排成一条直线，并使它们的间距正好是天狼星到地球的距离，那么把这个长度看成是一个圆周的直径，如果取π值取到小数点后100位的话，就可以把圆周长度精确到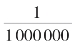
毫米。法国天文学家阿拉戈针对这一问题有自己的看法：“就精确度来说，如果圆周长度和直径之间有一个可以精确表示这个比值的数字，那对我们来说也可能毫无意义。”
其实在日常生活中用到π值时，只要记住小数点后两位（3.14）就够了，如果是需要更精确的计算，那么就需要小数点后四位（3.141 6：根据四舍五入的原则，最后一位数由5进6）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
