蒙上眼睛,你还能保持直线走吗？(几何学的趣味)

如果在暴风雪或大雾弥漫的恶劣天气下行走在荒漠戈壁上，旅行家手里又没有指南针这样辨别方向的装备，那么在这种无法判定方向的情况下，他们走来走去只会永远在绕圈子，走一会儿又发现走到了刚才走过的地方，永远都走不出去的样子，这样就迷路了，在这种情况下是很危险的。人们发现，这个时候步行者的兜圈子的大小大概为直径60到100米的一个大圆，如果走得速度快一些，偏离程度越大，圆圈的半径也会变小。

下面这个实验就是人们做的有关步行者不走直线走弧线的情况，这样专门的实验还有很多，让我们先来看一个实验的情景：

有一百名将要成为飞行员的人站在绿色的机场上，他们整齐划一地排列着，然后将他们的眼睛蒙住，一个个被蒙住眼睛的飞行员听到一声齐步走的口令后，便一起向前走去。结果，没过一会儿，就看到有的人开始往左，有的人开始往右，到后来，本来整齐的队伍乱作一团，甚至有的人开始原地打转，一直在走自己走过的路。

上一节中，我们讲了关于待在没有一点光亮的房间里的马克·吐温在屋子里一直转圈的糊涂事情，也是一个活生生地向我们展示这个奇怪的现象的例子，连科学家也无法在黑夜里走直线。的确，生活中这样的事情很多，当人们被蒙住眼睛后，他走路的方向会立刻没有了头绪，他会走得曲里拐弯，或者干脆在原地转圈，可他们自己却全然不知，反而觉得自己一直在往前走（图8-4）。

图8-4 蒙着眼睛行进

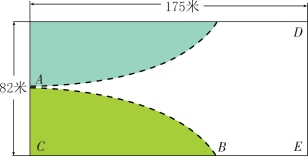
图8-5 威尼斯圣马尔克广场的实验示意图

在威尼斯的圣马尔克广场上曾经做过一个非常有名的实验，和前面飞行员的实验类似。这次找来一些市民，将其中一些人的眼睛蒙起来，让他们从教堂广场的一端走向另一端，这一段距离其实只有175米，这样短的距离，蒙上眼睛的人们竟然没有一个人走到终点，所有的人都不知为何歪到一边去了。如图8-4所示，他们好像都设定好了一样走着弧线，更有人撞到了旁边的柱子上。

《主人和雇工》一书中列夫·托尔斯泰也有过这样一段描写，生动地回放了迷路的人转圈的情景：

这时候，大雪依然在下，风变得更大了，瓦西里·安德烈伊奇骑在自己的马上，扬鞭策马地往前奔跑着，他觉得自己正在往树林里护林小屋的方向前进着。不过大片的雪花迷住他的双眼，狂风好像在和他作对，他只能不断地将身子放低，辕枕之间十分冰冷，只能把皮袄不断塞在身子下面，暖和一些，同时不断策马向前。

就这样，不断往前奔跑着，时间一分一秒地过去，他总觉得已经走了很久了，但是被大雪笼罩的荒原上，他除了马头什么都看不到，除了在耳边呼啸的风声，什么也听不到。他好像走进了一个白雪的世界，这里没有任何人，只有他和他的马。

就在这白雪皑皑的世界里，突然，眼前一片黑黑的东西让他兴奋起来。他高兴地跳起来，立刻策马向这一团黑黑的东西奔去，他以为看到了护林小屋的院墙，但是这个黑色的东西在空中摇摆着，并不是静止的，显然这并不是小屋。他走近一看，原来是一撮高高的蒿草，蒿草从积雪下面顽强地钻出，长在田埂上，在风中尽情地摇摆着，狂风将它压倒在地上，风吹过发出呜呜呜的声音。狂风对蒿草的折磨使瓦西里·安德烈伊奇心头一震，仿佛这个时候自己就如同蒿草一般在与这狂风和大雪做着斗争。他继续策马向前赶去，但他没有想到的是，他在走向这个蒿草的同时也改变了方向，心里想着是往小屋的方向前进，其实不知已经偏离很远走到另一边去了。

没过一会儿，又在前面的地方看到了一片黑色的东西，瓦西里·安德烈伊奇又高兴起来，他觉得这次一定是来到村庄小屋的地方了，可是驱马过去定睛一看，竟然又是一撮高高的蒿草，依然是在田埂上迎风摆动，看起来令人害怕，这时候他惊奇地发现，在这蒿草旁边有几个模糊的马蹄印，虽然被雪花盖住了部分，但还依稀可见，他走到那个马蹄印旁边，蹲下来仔细观察，发现这印记不是别人的，正是自己的马留下的痕迹。这样看来他刚才一直在转圈，不过这圈不大，没一会儿就回到了原地。

关于这样的小说情节还有很多，如果你读过儒勒·凡尔纳的《哈特拉斯船长历险记》，里面这一段情节你应该大概还有印象，那是一段关于在荒无人烟的雪原上旅行者迷路后原地打转的情节：

“我的朋友们，你们看，这是我们自己的脚印啊！”博士让大家看脚下，大声喊道，“看来我们是在大雾里迷路了，看，我们走来走去又走回来……”

探险家们在探险的时候发现，很多动物也有这样迷路的情况。比如他们在冰雪荒原上坐在雪橇上，拉雪橇的动物也是经常走大圈儿，如果将小狗的眼睛蒙住然后放入水中，它们也会在水中打圈圈，而天上的飞鸟如果眼睛瞎了，也会飞成圈圈。这也是为什么被猎枪打伤后受到惊吓的野兽逃窜的时候跑的不是直线是螺旋线，它们失去了判断方向的能力。

动物学家告诉我们，很多生物的行迹都是弧线的，包括蝌蚪、水母、螃蟹，甚至是水中的很多微生物也是这样的。如果说现在人们有照明设备和辨别方向的设备，在黑暗的森林或者荒原上不太容易迷路，不过这对于常年生活在荒漠草原或者海洋等地方的动物们来说，可是一件大事。如果它们一直原地转圈，就很有可能影响它们的生活，甚至危及它们的生命。正是这样的原因，像一条无形的链锁拴着动物们，让它们永远都不会远离自己的家乡。所以，即使闯入荒原的狮子也会回到原来的地方，即使把巢穴搭在峭壁上飞去大海中的海鸥也还能够回来找到自己的窝，有的鸟类让我们十分惊讶，它们竟然能够飞越海洋。

那么，为什么人们或者是动物在黑暗中无法保持直线运动而经常打转呢？

在提出这个问题之前，我们先要了解一下，如果想要走直线的话需要具备哪些条件呢？如果直接提出打转的问题似乎就缺少了神秘感。

这里我们可以想一下，那些装有发条的小汽车，小时候我们玩的时候发现它们有时候并不听话，它们经常无法直行而到处乱跑，小汽车跑曲线的现象其实很好解释，大家也不觉得有什么神秘，这是因车的轮子不一样大而导致的。

由此看出，如果人或者动物两侧的肌肉运动时完全一致的话，那人和动物自然也能不需要眼睛的帮助而走直线。不过我们都知道，人和动物的身体发育和生长是无法完全均衡的，很多人都是右侧身体的肌肉发育比左侧强壮一些。所以，如果一个人的右腿迈出的步子比左腿稍大的话，那么他行走的时候无法走直线就是很正常的事情了。在没有眼睛的帮助下，就无法修正走偏的路线，所以不可避免地就会一直向左偏移。这就和划船是一样的，我们右手划桨的力量要比左手有力很多，根据几何学原理也知道，这样船的方向会向左偏斜。

不过如果你是左腿比右腿迈出的距离大的话，如果每次多迈一毫米，走出一千步后，左腿就会比右腿多迈出一米，所以这样走出来就是两个相同圆心的圆圈，想要使两条腿走平行的直线是不可能的。

在1896年，挪威一位名叫古德贝克的生理学家对蒙眼转圈这个现象进行了专门的研究，并且也通过很多真实的实例进行认真的验证，下面让我们来看他搜集的两个例子。

在一个风雪之夜，如果有三个人在哨岗值班，他们想要回家就要走出宽4千米的山谷。如图8-6所示，他们的家在图上虚线所指的方向。但是在回家的途中，他们都不知不觉地偏向了右面，根据他们自己的速度计算一定时间内应该是可以走到家里了，可实际上，他们非但没有到达目的地，反而重新回到了哨岗的棚子，于是他们又重新上路，但是这一次偏移得更厉害了，比上次还快就又回来了。就这样，他们又一次出发，又一次回来，这样来来回回了五次，结果都像之前一样，于是他们放弃了回家的想法，只能在哨岗的棚子里等到天亮以后再回家。

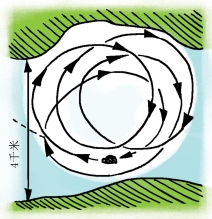
图8-6 三位值勤者迷路示意图

还有一个例子。在一个大雾弥漫的晚上，天上看不到星星，没有一点光亮，在这样的情况下，如果是在大海里，那么想要划船走直线也是一件十分困难的事情。一个人在这种天气下，想要横渡海峡，如图8-7所示，他想要横渡宽4千米的海峡，在雾气的笼罩下，他无法辨别方向，只能一直向前划去，本以为已经到达了岸边，却一直都没有看到海岸，反而是在大海里转圈，转来转去竟又转回到刚才自己出发的地方。

(www.xing528.com)

图8-7 在大雾的天气里划船横渡海峡

其实我们可以算出之前例子中他们的左腿比右腿到底迈出的每一步到底长多少，就拿刚才介绍过在雪谷里转圈的平面图来计算，由于他们行进中是向右偏斜，我们很容易知道，他们的左腿要比右腿迈得长一些。人在行走的时候，左右两脚的足迹线之间距离大概是10厘米左右，如图8-8所示，当人走出一个整圆，这时候他右腿所走过的路为2πR，左腿所走的距离为2π（R+0.1），式中R为这个圆周的半径，单位为米。那么2π（R+0.1）和2πR的差数为：

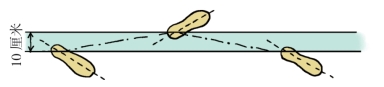
图8-8 行走时左右脚的足迹线

2π（R＋0.1）－2πR＝2π×0.1,

求出的结果为0.62米，也就是620毫米，这个差就是左右迈出步子长度的差。由于两条腿重复的次数也就是我们的步子数目，所以从图中就可以得出，这几个人兜圈子所转的圆圈直径大概是3.5千米，周长也就是一万米左右。如果每一步的步长平均为0.7米，那么这段路也就走了≈14 000步，两只脚各迈七千步，不过我们知道，我们的左脚右脚所走的七千步是不一样的，左脚要多走620毫米。

左脚每迈出一步就要比右脚多出毫米，还不到0.1毫米。脚步上的差别就这么一点点，却导致如此惊人的结果。

所以左右两腿迈出的步差决定了迷路的人走出的圆圈半径，也就是兜圈子的圈子大小。这样的关系式很容易明白，比如在步长为0.7米的时候，那么这个圈的长度迈出的步数也就是其中R为圈的半径，单位为米，左右两腿迈出的步数为左右两腿是相同的，如果用这个步数与步长的差x相乘，那么就可以算出左右两腿分别走出的同心圆圆圈的差值：

或者

Rx=0.14，

式中的R和x的单位为米。

我们根据这个简单的公式，以及已经知道了步子的差的值，那么圆圈的半径就很好算出来了，同理，如果知道半径也可以求出步差。在之前的例子中，那些在圣马尔克广场做实验的人们，他们所走出的圆的半径最大是多少呢？如图8-5所示，这些人中没有一个人走到教堂另一边，也就是DE一边。根据AC这个圆圈的高41米，和没有达到175米的半弦的长度，那么就可以算出最大半径。通过上面的数据可以得出下面的等式：

BC2＝2R×AC- AC2

如果已知BC=175米，那么就可以得出：

也就是说可以算出它的最大半径大约为394米。

我们已知了最大半径的大小，那么从上面得出的公式Rx=0.14中可以算出步差的最小值：

394x=0.14，

由此算出：

x≈0.4毫米。

实验结果表明，参加实验的人左右两腿的步差不小于0.4毫米。

从图8-9中可以看出，当人在前进的时候，迈出的每一步角度都是相等的，这就说明角B1=角B。这个时候，A1B1总是等于AB，而B1C1总是等于BC，所以这个时候三角形A1B1C1和三角形ABC相等，那么就可以知道，AC=A1C1。相反，如果在行进的过程中其中一条腿比另一条迈出略远，即使两腿的长度是一样的，但是步长也是不一样的。所以有时候我们经常听到一些错误的解释，他们觉得实验中的人之所以盲目地转圈是因为左右两腿的长度不一样长，因为大多数人右腿比左腿都略短一些，他们认为这是导致这些人在行进的时候不走直线发生偏离的原因，其实这个错误是违反了几何学的，因为在这中间起作用的不是两条腿的长短，而是步差在这里起到了重要的作用。

图8-9 如果每步的角度相同，步长也就相等

这个道理同样适用于在湖中划船而发生偏离的现象，船向左偏甚至转圈是因为划船的人右臂的力量比左臂大，才会产生这样的偏移。在不能用视觉来判断直线运动的时候，那些左右脚步长短不一、左右翅膀用力不等的动物，即使它们的两脚、两翅膀力量差很小，但也会原地打转。

这样看来，如果人或动物在不用自己的眼睛控制方向的前提下还可以保持直线运动，是非常奇怪的。从上面的各种例子和解释中，我们可以看到不走直线是很正常的现象。如果想要进行直线运动，那么身体的各个部位都需要严格的对称，这对于生物界来说基本是不可能的事情，有一点点的偏差都会造成曲线运动，所以我们这里谈论的事情是我们过去以为是很平常的事情。不过这些干扰对于聪明的人类基本上是没有障碍的，因为他们可以用指南针、地图等帮助判断方向的设备来避免这个问题。