马因·里德小说里的几何计算误差分析

几何学的天才们一定知道马因·里德小说里的少年主人公所运用的计算两个圆台体体积的方法并不精确。假设两个小一些的底面的半径为r（图8-2），大的底面半径为R，木桶的高度为h，是圆台体高度的两倍，那么容积为：

这个圆台体的容积可由公式得：

这两个算式相比，第二个算式大于第一个，两者相差：

根据在代数中学到的知识可知，（R－r）2为正数，也就是说，少年计算的结果略小于实际情况。

如果能确定他计算出的结果比实际情况小多少，那就更有意思了。观察木桶的形状，桶身最粗的部位比它的底面直径大，也就是说，如果马因·里德小说里的木桶就是这种形状，那么就能算出这两个截圆锥体得出的容积和实际情况之间的差：

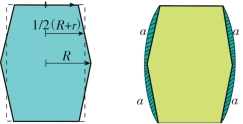
图8-2 验算少年计算出来的结果

假设π值为3，上述算式＝由此可以看出，少年的计算误差等于一个圆柱体的容积，它的底面半径是木桶的最大截面半径，高度是木桶的。

由于木桶的容积要比两个相叠的圆台体容积大些，所以我们要把这个计算结果加大一些。如图8-2（右）所示，用上述测量方法测量容积的时候，表示容积的字母a、a、a、a的部分都被去除了。(www.xing528.com)

这个计算木桶的容积的方法并不是只有马因·里德笔下的少年想出来了，它还应用于很多求木桶近似容积的题目中。其实要想算出木桶的准确容积是很困难的，德国天文学家开普勒也曾试着解决这一难题，在他的著作中，就有论述测量木桶容积方法技巧的专著。到现在为止，也没有找到解答这类题目更精确的方法，用现在的公式求出来的都是近似值。比如法国南部通常使用这个公式：

木桶容积＝3.2hRr，

这个公式经过实验证明是适用的。

再来研究一下这个有趣的问题：为什么要把木桶设计成一个两侧鼓出来的圆柱体呢？这样的形状是非常不便于测量的。如果把它加工成一个标准的圆柱体不是更便于计算吗？其实这样形状的桶是有的，但大多都是金属的，而不是木桶，这就引出下一道题来。

题：为什么要把木桶加工成中间鼓的不规则圆柱体呢？这样的形状有什么优势吗？

解：这样的形状优势就在于可以使桶箍紧紧地箍住木桶。锤子敲打桶箍时，桶箍就会接近木桶鼓起的位置。这时桶箍就就把桶的拼板箍紧，保证了木桶的牢固性。

木制的水桶、水盆等物体由于种种原因通常都不是圆柱形状，而是圆台体形状：这个方法很简单，却能把这些中间鼓起的制品箍得结结实实（图8-3）。

图8-3 把桶箍敲向凸肚部分，可以把桶箍紧

在这里，我们可以来看一下开普勒对于木桶这一物件的论述。这位伟大的数学家在发现行星运动的第二和第三定律间的时期就留意到了木桶形状的问题，还针对这个问题撰写了一篇数学论文：《酒桶的立体几何学》。开篇内容如下：

酒桶的制作材料、要求和它的用途，都采用了和圆锥体与圆柱体相似的圆的形状，液体如果长久地保存在金属容器里就会因铁锈而变质；而玻璃和陶制的容器不够结实，而且尺寸又略显小；石制容器太重了，不适合装液体。所以说木制容器盛装和保存酒这种液体是最合适不过的了，把一个粗大树干掏挖出容量体积和酒桶相同的一个容器是不现实的，就算这样制作出来了，也会干裂的。因此制作木桶要用一片片的木条拼装成，要使液体不从木条间的缝隙渗漏出来，却不能用别的材料，那么唯一的办法就是用桶箍把桶箍得紧紧的……

当然了，最好能用木板拼出一个球体的容器，但根本不可能。把木板箍出一个标准的圆柱体，那么它就很容易箍松了，这样这个桶就制作失败了，而且也不能把它们箍得更紧了。如果木桶是从桶的最鼓处向两个底面方向收缩的圆台体的形状，只有这个样子，桶箍松了才能向粗处移紧。这样形状的木桶方便储存液体，用大车运送时也很方便，而且它看上去是上下两个彼此相像的部分组成，方便滚动的同时，也非常美观大方^[3]。