正弦函数的计算方法及数值表

我们在这一章里要研究如何不用公式和函数表，只用正弦函数的概念计算出精确到2%的一个三角形的边长和精确到1°的三角形内角角度。当你在野外郊游时，公式记不全，又没带函数表时就会用到这种简便三角学的计算方法了。鲁滨孙在荒岛上时就经常用到这种三角学。

假设你没有学过三角学或是以前学过但现在忘了，我们可以从这章内容重新学起。什么是直角三角形的锐角正弦？它是锐角的对边和弦长之比，例如，a角的正弦（图5-1）由此可以看出，三角形ABC，ADE，AB′C′和AD′E′都是相似直角三角形，上述这些比值都是相等的。

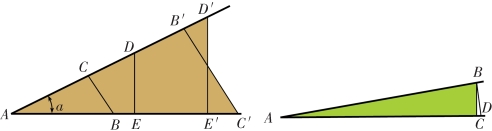
图5-1 什么是一个锐角的正弦函数

从1°到90°的所有度数的正弦函数值分别是多少呢？这个问题其实非常容易：只要自己画一张正弦函数表就可以了，现在咱们一起来做这个表。

我们可以先来研究几何学中学到的正弦函数角度，90°的正弦函数等于1，45°角的正弦函数可由勾股定理计算出来，为就是0.707。30°角的对边长度是弦的一半，所以30°角的正弦函数为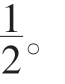这时我们就知道三个角度的正弦函数值了（正弦函数值用sin来表示）：

sin30°＝0.5,

sin45°＝0.707,

sin90°＝1。

只知道这几个角度的正弦函数值还远远不够。还要把中间每隔一度的角度正弦函数值计算出来。计算正弦函数值时，为了减小误差，可以用弧和半径的比来取代对边与弦的比。如图5-1右所示，的值相差非常小，这个差值很容易就能计算出来。如1°角所对的弧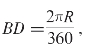所以sin1°为：

同理可计算出：

sin2°≈0.034 9

sin3°≈0.052 4

sin4°≈0.069 8

sin5°≈0.087 3

如果没有误差，这个数值可以一直往下计算，当计算到sin30°时，计算出来

的数值不是0.500，而是0.524，这个误差就有可能是也就是大约5%的误差。虽然野外旅行进行测量计算时不需要十分精确，但这个误差仍然是比较大的。所以用上述方法计算正弦函数值就要找到它允许的极限，我们可以用精准的方法计算出15°角的正弦函数值。可以先做一个简单的图（图5-2）。假定sin15°＝延长BC至D点；把点A和点C连接起来，由此得到两个全等三角形ADC和ABC，还得到了一个与30°相等的角BAD。画一条线段BE，使它与AD垂直，由此得到直角三角形BAE，角BAE为30°，那么BE＝。在三角形ABE中，由勾股定理得出AE：

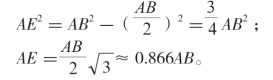
也就是说：ED≈AD－AE＝AB－0.866AB≈0.134AB。由三角形BED计算出BD：

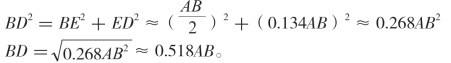
BD的是BC，所以BC＝0.259AB，所以，15°角的正弦函数值为：

(www.xing528.com)

图5-2 sin15°的计算方法

如果近似值只取到三位的话，那么sin15°的正弦函数值就是这个数值。但这是根据以前的方法计算出来的近似值，为0.262,比较0.259和0.262这两个数值时，你会发现如果取似近值时只取小数点后两位，那么这两个数值的近似值（0.26）是相等的，在近似值0.26取代0.259时，出现的误差仅为是大约0.4%。在野外进行测量时这样的误差是完全允许的。所以可以根据这个近似方法求出1°到15°的正弦函数值。

利用比例关系，可以计算出15°到30°之间各度数的正弦数值，想一下，sin15°和sin30°之间差为0.50－0.26＝0.24。假设每增加一度，它的正弦值增加的数值就是这个差数的，就是这个结果严格来讲的确不准确，但它的误差只在第三位小数点上，而我们只用到两位小数点。所以把0.016加到sin15°的数值上，就计算出了16°、17°、18°等度数的正弦函数值：

sin16°＝0.26＋0.016＝0.28，

sin17°＝0.26＋0.032＝0.29，

sin18°＝0.26＋0.048＝0.31，

… …

sin25°＝0.26＋0.16＝0.42等。

这些角度的正弦函数值前两位小数是准确的，这对我们来说就足够了：这个数值和精确的正弦函数值只差最后第三位小数的一半，就是0.005。

这个方法也能用于计算30°到45°之间度数的正弦函数值，sin45°到sin30°之间的差为0.707－0.5＝0.207。把这个差除以15，为0.014。再把这个数值加到30°的正弦函数值上，就得到：

sin31°＝0.5＋0.014＝0.51

sin32°＝0.5＋0.028＝0.53

… …

sin40°＝0.5＋0.14＝0.64等。

现在只差求出45°以上锐角的正弦函数值了，在这里，又要用到勾股定理了。例如要求53°角的正弦函数值，就是的比值（图5-3）。由于角B为37°，所以可由上述方法计算出它的正弦函数值为0.5＋7×0.014＝0.6。另外，我们知道则＝0.6，所以AC＝0.6×AB。AC值求出来了，那么BC值为：

所以

总之，只要你会开平方，就会熟练地进行这样的计算。

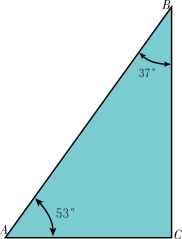
图5-3 计算45°以上度数的正弦函数值