这个问题可以借助计算公路弯道半径的公式的帮助进行解答。
从前面那道题目可以知道，确实存在水山，但不能从物理学的角度去理解这一说法，要从几何学的意义上去理解。其实一个海或湖泊都可以称之为“水山”。站在湖边时，你的视线会被凸起的水面挡住，使你看不到对岸的一点，湖面越辽阔的情况下，凸起的水面就会越高。这个高度我们可以计算出来：矢的长度可以由公式
得出为h＝
公式中a是两岸的直线距离，也就是湖的宽度，假定湖宽为100千米，则水山的高度为：
这座水山竟然那么高！
就连一个阔度只有10千米的湖也是个凸起2米的水山，都超过了人的高度。
那么我们称凸起的水为“山”妥当吗？
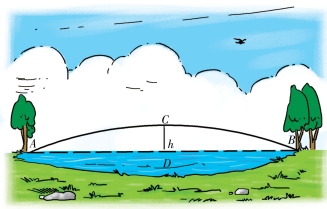
其实这在物理学上是不妥当的，因为这些凸起并没有高出水平面，所以说，这些凸起只能算是平原。如图4-9所示，不要认为直线AB是一条水平直线，弧ADB在它之上。其实ACB才是水平线，而不是AB，因为它和静水的表面相重合了。而直线ADB则是倾斜的斜线：AD线朝“地表”下方最深的点D点倾斜，接着再重新向上升起，在B点从水下浮出来。如果沿着直线AB铺设一条管道，从A点放进管道里一个球，球就会向下滚动（如果管道壁很光滑），一直滚到D点，再从这里滚向B点；接着它会再滚回到D点，一直到A点，就这样周而复始地滚来滚去。这个小球会沿着管道壁永远地滚来滚去（在没有妨碍物体运动的空气存在的情况下）。
(www.xing528.com)
图4-9 水山示意图
ACB看上去像一座山，但在物理学上，它只是一块平地，只有在几何意义上，它才是一座“山”。
【注释】
[1]有的人可能这样认为，坡的长度AB与水平线AC不可能相等，但你要知道一点，BC只是AB的0.01，AC和AB之间的长度差非常小。根据勾股定理可得：
两者长度仅差0.000 05。若是计算时只求近似值，那么这样的误差大可以忽略不计。
[2]在实践中求直径时，经常会把除法改成乘法，就是乘以除数的倒数0.318，在求半径时，就是乘以0.159。
[3]普希金著作《吝啬骑士》，选自普希金戏剧集，戴启篁译。广西：漓江出版社，1982年。译者注。
[4]由于弯道半径非常大，测量弦的绳子需要非常长，所以此方法在实际应用中会有不便。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
