船头劈开的波峰-趣味几何学成果

再回到河边，站在桥上观察轮船快速驶过时你会发现，船头在水面上劈开了两道波峰（图2-24）。

图2-24 船头劈开的波峰

为什么会出现这两道波峰呢？为什么船行驶得越快，这两道波峰形成的角度越小呢？

想把这个问题弄清楚，可以从投入水中的石子在水面上产生不断扩散的圆形波纹开始研究起。

如果每隔一段时间就往水中投一块石子，水面就会出现很多大小不一的圆圈。激起圆圈最小的是最后投入的石子，如果沿着一条直线往水中投石子，这些圆圈就会在船头的两侧形成波峰。投得越快，投的石子越小，两者就越相似。

把一根木棍插入水中划动的效果就是连续不断地往水中投石子的效果，就能看到船头劈开的那种波峰。

这时只要对这个画面稍加补充，你就明白了。船头劈开水面的时候，会产生无数次像往水里投石子的圆形波纹。轮船向前行驶，就会连续不断地出现无数个图2-25所示的这样的圆形波纹。相邻的波峰在一起相互碰撞。没有碰撞到的地方就只有在波峰外圆周上的两小段，这些小段合为一体，在这些圆形波纹的外切线内形成两道波峰。

快速移动水面上的物体，它的前端都会产生像船头劈开的波峰（又称水脊）。(www.xing528.com)

所以可以得出：只有物体在水里移动速度比水浪更快时才会出现这种波峰。如果用木棍在水里划动，是不可能出现波峰的，因为波纹是一个套着一个的，无法形成圆形波纹的外公切线。

河水从一个静止的物体前端流过，这时可以看到物体前端散开的波峰，如果水流湍急，在流经桥墩的部位也会有波峰出现，由于它们受力均匀，没有被旋转的螺旋桨破坏，所以这里的波峰甚至比船头劈开水面产生的波峰更加明显。

懂得波纹形成的几何学原理了，现在来解这道题。

题：什么决定了船头劈开的两道波峰角度大小？

解：以圆形波纹的中心向公切线的切点引出半径（图2-25，右），就是说O1B是船头部分在某段时间里走过的路程，O1A1是流波在同一时间内扩展的距离。O1A1与O1B之比是角O1BA1的正弦，和波浪速度与船速的比例相等。也就是说，两道波峰间的角B是两倍的角O1BA1，它的正弦约为圆形波浪扩展的速度和船速的比例。

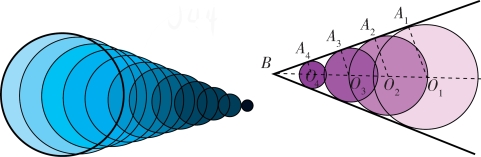
图2-25 船头的浪波形成过程

各种船舶的船头劈开的波浪扩展速度都差不多，所以，是轮船的速度决定了两道波峰角度大小。反之，根据船头劈开的波峰角度也可以判断出船速比波浪速度快多少。比如两个波峰间的夹角为30°（客轮和货轮大多是这个角度），则它的半角正弦（sin15°）是0.26，所以说，船速比圆形波浪的扩展速度快约为3倍。