水面上的圆圈展现神奇

题：你可能经常看到这个现象，把一颗石子投入水中，静静的水面会出现一圈一圈的圆圈（图2-22）。

图2-22 水面上一圈圈的圆圈

是的，你可能一直认为这是一个简单的自然现象：石子在水里激起的波浪会向周围散开，所以每一圈都是从这个点散发出去的，都处于同一个圆周上。

上述是石子投在静水中的情况，如果在流动的水中会怎样呢？在湍急的河水中投入石头也能激起圆圈的波纹吗？还是形状被拉长了的呢？

猜想一下，在流动的水中，圆形的波浪应该会向水流动的方向伸展；扩散的速度应该是顺流快过逆流。所以，水面起的波纹不会分布在一个圆周上，而会在一个拉长了的封闭曲线上。(www.xing528.com)

其实不是这样的，你往流动的水中投入石子，就会看到它激起的圆圈和在静水中的一样，这是什么原因呢？

解：解答这道题。如果水静止，波纹是圆形的，水流会有什么变化？水流把圆形波纹的每个点都吸引到箭头所指的方向（图2-23），并且所有的点都往前移动相同的距离，而这种移动不能改变图形原本的形状。要使点1（图2-23，右）到了点1′的位置，点2移到点2′……四边形1′2′3′4′最终代替四边形1234。从四边形的几个点可以看出，两个四边形是相等的，如果起初在圆周上取的是多点，得到的将是相等的多边形，若取的是无数点，那么将得到两个相等的圆周。

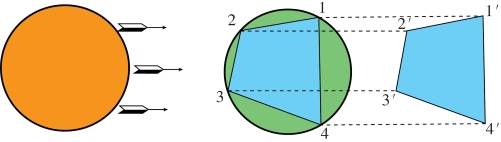
图2-23 波纹的形状并不会随着水的流动而改变

所以波纹的形状仍是圆形，不会随着水的流动而改变，区别只在于在静水中，圆圈不会移动（不包括圆形波纹以同一中心向四方扩散）；在流动的水面上，圆形波纹会和水流一同移动。