如何使用大头针测量河流宽度

不渡河却要测量河的宽度，在一个懂得几何学的人眼里就像不用爬树就测量它的高度一样简单，我们要测量无法逾越的距离仍然要利用测量无法接近的高度的方法。这两种情况都是用其他距离的便捷测量来取代未知距离的测量方法。

解决这个问题有很多种方法，下面我们来介绍几种最简单的方法。

1.第一种方法，我们都熟悉“大头针测高仪”，在这里我们要用到它，把三个大头针钉在等腰直角三角形的三个点上（图2-1）。想要测量河流宽度AB（图2-2），我们无法到河的对岸，只能站在点B的河岸边，你拿着“大头针测量仪”站在点C处，一只眼睛望向两枚大头针的方向，使B、A两点和大头针a、b两点在同一直线上。如果你是这样的，那你就站在AB的延长线上。这时扶好仪器，眼睛看向b、c两点（与刚才的方向垂直），你会看到点D在bc的延长线上，被bc点遮住。然后在C点用木条做好标记，拿着工具沿着CD直线走，直到找到E点为止（图2-3），在这一点可以看到b遮住了C点的木条，a遮住了A点，这就说明你找到了三角形ACE的第三个顶点。在这个三角形中，角C是直角，角E是“大头针测量仪”的锐角，就是直角的1/2。那么A角也是直角的1/2，所以AC＝CE。如果你简单测量了CE的距离，你就会知道AC的距离，BC距离可直接测量得知，AC的距离减去BC的距离就是河流的宽度了。

图2-1 用大头针测量仪对河流宽度进行测量

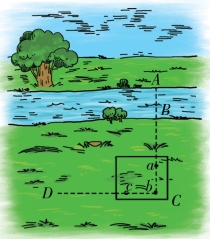
图2-2 大头针测量仪的第一个位置

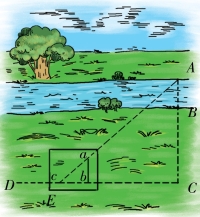
图2-3 大头针测量仪的第二个位置

但拿着大头针测量仪一动也不动是很不容易的事，所以最好把带有大头针仪的小木板钉在一根木杆上，再把木杆垂头插进地面固定好。

2.第二种方法和第一种方法相似，先在AB延长线上找到C点，再借助大头针测量仪的帮助找到CD直线，使它与CA垂直成直角。接下来的做法与第一种方法有所不同（图2-4）。在CD线上标出CE和EF，并使两者长度相等，在E、F两点上钉上木条为标记。然后拿着大头针测量仪站在点F处，找到和FC线垂直的方向FG，沿着FG的方向向前走，找到这条线上的H点，从这点看点A，发现A点正好被E点的木条挡住，也就是说，H、E、A三点都在同一条直线上。

图2-4 利用全等三角形的特性测量河的宽度

问题就解决了：FH和AC的距离相等，只要用FH值减去BC的长度就是河流的宽度了（你一定知道FH和AC相等的原因）。

用第二种测量方法需要的场地比第一种方法大，如果有足够的场地条件使用两种方法，可以用一种方法验证另一种方法。(www.xing528.com)

3.第三种方法。第三种方法就是把第二种方法稍微改动一下的结果：在CF线上量出两段不相等的距离，其中一段比另一段长几倍，如图2-5所示，使EC比FE长3倍。接下来的做法和第二种方法相同。沿着和FC垂直的方向找到H点，从这里看A点，会发现A点被E点挡住了。但这里FH和AC并不相等，只是AC的。因为ACE和EFH两个三角形只是相似三角形，并不相等（各角相等，但各边不相等）。根据三角形相似的关系，可以得出：

图2-5 利用相似三角形的特性进行测量

AC∶FH＝CE∶EF＝4∶1。

所以，测量出FH的距离后，再乘以4，就是AC的长度，再减去BC，就是河流的宽度了。

是的，这个方法比第二种方法需要的场地小，使用起来更便利。

4.第四种方法。这个方法是根据直角三角形的特性进行测量的，就是如果三角形的锐角之一是30°，那么这个角所对的直角边的长度就是斜边的一半。想确定这点是很容易的，假设直角三角形的ABC的B角（图2-6，左）是30°，所以，AC＝AB。以BC为中心，把三角形ABC旋转到和它初始位置对称的位置（图2-6，右），构成三角形ABD，因为C点的两个角都是直角，所以ACD线是直线，三角形ABD中，由于角ABC和角CBD都是30°，角A＝60°，所以角ABD＝60°，那么两个相等角的对边也相等，AD＝BD，由于AC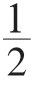＝AD，所以AC＝AB。

图2-6 直角边等于斜边一半的情况

测量时，想要利用三角形的这个特性，就要在木板上固定好大头针的位置，使它成为一个直角三角形，并且使其中一条直角边的长度是斜边的一半，拿着这个仪器站在点C处（图2-7），使A点在大头针仪上的斜边延长线上，在直角三角形的短直角边bc的延长线上找到E，使得EA和CD相互垂直（这一步骤可用大头针仪轻松做到）。那么CE边的对角是30°，则CE是AC边的测量出CE的长度，乘以2，再减去BC的长度,就是河流的宽度了。

图2-7 用锐角为30°角的直角三角形进行测量

刚才说的四种测量方法简便易行，不需要渡河就能测量出河的宽度，准确度也很高，还有一些方法需要使用复杂的仪器（包括自制的），在这里就不多介绍了。