万能公式的实际应用-趣味几何学

这种万能公式是存在的，它适用于圆柱体、圆锥体和圆台体甚至任何类型的棱柱体、棱锥体和棱台体，包括球体，这个公式就是著名的数学公式——辛普森公式：

公式中：h是立体的高度，b1是下底的面积，b2是中部的截面积，b3是上底的面积。

题：证明上述公式确实可以计算出棱柱体、棱锥体、棱台体、圆柱体、圆锥体、圆台体和球体这七种几何体的体积。

解：如图1-17所示，只要在上述几种几何体的体积运算中运用该公式，就能证明该公式的正确性了。

如图1-17（a）所示，在棱柱体和圆柱体中运用可以得出：

如图1-17（b）所示，在棱锥体和圆锥体中运用可以得出：

如图1-17（c）所示，在圆台体中运用可以得出：

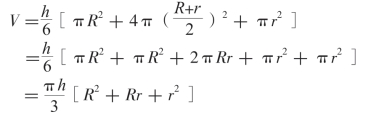
如图1-17（d）所示，应用于球体，与截锥体的证明方法类似，得出：

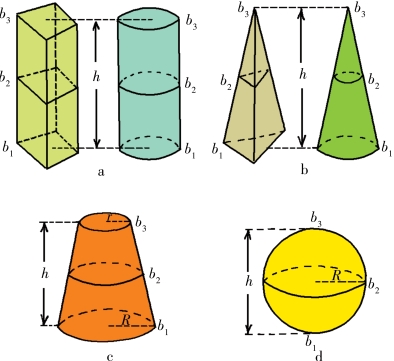
图1-17 用一个公式计算出几种几何体的体积(www.xing528.com)

题：这个万能公式有一个很有趣的特点，就是它还能计算平面图形的面积，如平行四边形、梯形、三角形。

其中：h是图形的高度，b1是下底的长度，b2是中间线的长度，b3是上底的长度。

那么，应该怎样证明呢？

解：如图1-18所示，把公式运用到计算中。

如图1-18（A）所示，在平行四边形中运用公式可以得出它的面积为：

如图1-18（B）所示，在梯形中运用公式可以得出它的面积为：

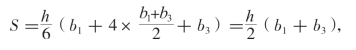
如图1-18（C）所示，在三角形中运用公式可以得出它的面积为：

这样看来，这个公式的确是万能公式。

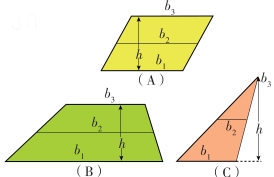
图1-18 用万能公式计算这些图形的面积