阴影长度测量物体高度，趣味几何学

小时候发生的一件事令我惊讶万分，直到现在还能回忆起当时的情形。那时，我看见一位看守林园的老人站在一棵松树旁，手里拿着一个小巧的仪器，正在测量松树的高度。老人透过仪器朝树梢瞄了一眼，我猜想接着他可能会带着链尺爬到树上去测量。没想到，老人不但没有去爬树，而且把仪器收起来，告诉大家测量结束了。

当时我还是一个小孩儿，觉得这种不用砍树，也不用爬树的测量方法很神奇，就像魔术一样高深莫测。后来，当我知道了几何学的基本原理后，才知道这种测量方法很简单。而且，利用简单的仪器或者徒手测量的方法多种多样。

既古老又简单的方法，就是公元前6世纪古希腊的哲学家泰勒斯测量埃及金字塔所用的方法，借助了金字塔的影子。当时，法老和祭司们聚集在最高的金字塔下面，看着眼前这位想要测量宏伟建筑高度的客人。据说，泰勒斯选择了一个时间来测量金字塔的高度——当他的身影的长度和身高相等时。因为这时金字塔的阴影长度^[1]也和它的实际高度相等，这就是类比的方法。

现在，我们会觉得古希腊哲学家的智慧也不过如此，他解决问题的方法连小孩子都知道。不过，大家不要忘记，我们是站在几何学的角度看待这个问题的，而几何学是泰勒斯之后的无数先人的智慧结晶凝聚而成的。希腊数学家欧几里得生活在距离泰勒斯很久之后的时代，他撰写了一部很好的书，之后的两千年，人们就是通过这本书来学习几何学的。虽然今天的每个中学生都熟知这本书中的原理，但是泰勒斯的时代还没有这些原理，他能够借助阴影测量金字塔的高度，必然知道三角形的一些特征，下面我们来说两个特性（第一个特性就是泰勒斯发现的）：

（1）等腰三角形的腰所对的两个角相等；反过来说也成立，那就是有两个角相等的三角形是等腰三角形。

（2）任意三角形的内角和等于180°。

由于掌握了这些知识，泰勒斯才得出，当他的身影长度等于身高时，太阳光以45°投射到地面上，由此可以得知，金字塔顶点、塔底中心点和塔影端点构成一个等腰三角形，塔影的长度和金字塔顶点到塔底中心点的线（也就是金字塔的高度）是三角形的两个腰。

在充满阳光的日子里，用这个简单的方法可以测量出独立的树木高度。不过，在高纬度地带，不会那么容易出现合适的机会。因为在那些地方，太阳总是低垂在地平线上，只有夏季的正午时分，物体的影子长度才和高度相等。因此，泰勒斯的测量方法有一定的局限性。

然而，在有阳光的日子里，只要把上面的方法稍作改动，就可以测量出任何物体的高度。当然，除了测量物体影子的长度，还需要知道自己的身影和身高或者竹竿的高度和影子长度，根据它们的比例，求出物体的高度（图1-1）：

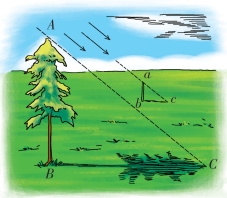
图1-1 根据树的阴影测量它的高度

AB∶ab＝BC∶bc。(www.xing528.com)

也就是说，树影的长度是你的影子长度的几倍，树的高度就是你的身高的几倍。当然，这个结果是根据三角形ABC和abc相似的几何原理得来的。

有的人也许会说，这么简单的方法不用从几何学中找依据。离开了几何学，人们就不知道树高几倍，树影就长几倍吗？不过，事实并没有这么简单。如果把这条规律用到路灯的投影上，这条准则就不适用了。从（图1-2）中可以看到，AB的高度大约是ab高度的2倍，但影子的长度BC是bc的7倍。没有几何学，你要怎么解释这种现象？为什么相同的方法会出现不同的结果？

图1-2 这种测量方法在什么情况下不适用

题：我们仔细想一想，这两者之间有什么区别。主要的问题是，太阳光线是平行的，而路灯的光线则是不平行的。后者的说法明显是对的，但怎样才可以确定太阳的光线是平行的呢？

解：我们之所以说太阳照射到地球上的光线是平行的，那是因为光线之间的角度小得可以忽略，只要用一个简单的几何学计算就可以证明。假设从太阳的某一点射出两道光线，落到地球表面的两个点上，两点之间的距离我们设定为1千米。以太阳上射出光线的那一点为圆心，太阳到地球的距离（150 000 000千米）为半径画一个圆，那么两道光线的圆弧长度是1千米。这个圆的周长是2π×150 000 000千米＝940 000 000千米。这个圆上的每1°的弧长是圆周的大约是2 600 000千米；1弧分是1弧度的，即43 000千米；而1弧秒则是1弧分的，即720千米。我们假设的圆弧长度是1千米，对应的角度应该是秒。最精密的天文仪器也无法测量出如此微小的角度，所以在实践中可以省略不计，我们认为到达地球上的太阳光线是平行的直线^[2]。

如果不清楚这些几何知识，利用阴影测量高度的方法就没有了理论依据。

当你把影子测量法应用到实践中的时候，就会发现这个方法不一定总是可靠。因为阴影尽头的界限不是十分明确，测量的长度不可能准确无误。太阳光投下的每一道阴影，尽头的轮廓都模糊不清，颜色暗淡，这就导致阴影的界限难以确定。为什么会这样呢？因为太阳不是一个点，而是一个巨大的发光体，可以从无数的点上发射出光线。从图1-3中可以看出，树影BC后面还有一段模糊的影子CD。点C和点D与树顶A之间形成的角度CAD，跟我们看太阳圆面所形成的夹角相等，即半度。由于阴影的不确定所造成的误差，即使是在太阳高挂在空中时，也可能是5°或者更大。这个误差再加上地面不平及其他难以克服的误差，使得测量的结果不够准确。例如，这个测量方法不能用在高低不平的山地上。

图1-3 半影是如何形成的