黄河年径流序列模型重构及预测研究

本节采用重构系统方程自适应预测模型和多重分支神经网络模型分别对黄河年径流序列进行短期和中长期预测。仿真过程和结果如下：

1.重构系统方程自适应预测

建立系统一般框架如式（6.9）所示。选择Lorenz混沌方程作为初始参考方程，其x（t）序列表现出和黄河年径流相似的空间结构，选Lorenz方程的一种转化形式为

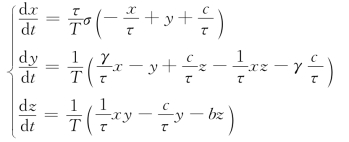
其中，T=13.41，τ=12.61，c=260，γ=28，σ=10，b=8/3。广义状态向量取为

X=[x1…x33]T=[x y z a11a12…a310]T

比较可得初始时刻a11=182.319，a12=—0.746，a13=9.403，a21=—43.051，a22=0.166，a23=—0.075，a24=1.538，a26=—0.006，a33=—1.538，a34=—0.199，a35=0.006。再取x（0）=487.0，y（0）=1.0，z（0）=3.0，即可确定该方程的初始条件。

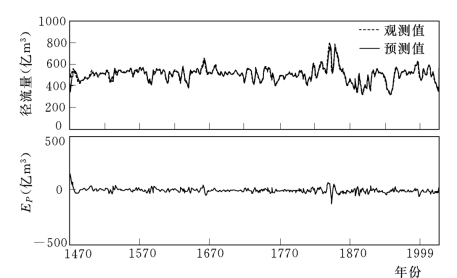
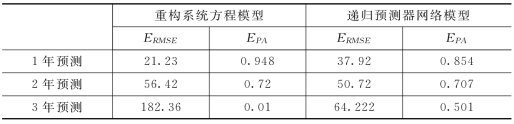
因为序列的采样时间为年，所以一步预测的预测期为一年。黄河年径流序列一步预测仿真结果如图6.18所示。定量的性能指标ERMSE值和EPA值计算见表6.4。可以看出，一步预测时，重构系统方程自适应预测法可以达到较高的精度，ERMSE=21.23，EPA=0.948。但随着预测期的增大，预测精度迅速下降，三步预测时，预测基本失败。这表明重构系统方程法适用于时间序列较短期的预测，较长期预测需要采用具有强大存储和记忆能力的神经网络方法。

(www.xing528.com)

图6.18　黄河年径流重构系统方程一年期预测的预测曲线及其误差曲线

表6.4　重构系统方程模型和递归预测器网络模型的预测性能

2.递归预测器神经网络预测

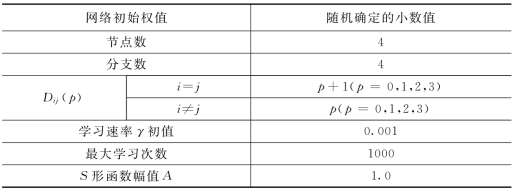
采用第5章介绍的方法，选取网络初始模型参数如表6.5所示。网络包括4个节点，节点间由4条分支连接，第4个节点的输出为网络输出。网络输入为x（t）=[x（t），x（t—1），x（t—2），x（t—3）]，网络输出为y（t）=x（t+η），η为预测步数。采用最近的110组输入输出样本对训练网络，实现一步或多步直接预测。

表6.5　递归预测器网络初始仿真条件

ERMSE值和EPA值计算见表6.4。相比较而言，对于短期预测，采用重构系统方程预测方法可以达到较高的精度；而对于中长期预测，采用递归预测器神经网络方法的预测性能较好。