【摘要】：混沌学的发展为分析黄河径流运动特性提供了一个全新的思路。取斜率平均值即可得到黄河年径流序列的关联维数为2.9。图6.17年径流最大Lyapunov指数的计算λ1为正数，D为正小数，表明该序列可能具有混沌特性；λ1值较小，表明该序列的邻近吸引子轨道离散度较低，因此有可能进行较为长期的预测。
混沌学的发展为分析黄河径流运动特性提供了一个全新的思路。本节通过计算描述混沌系统的重要特性指标，包括最大Lyapunov指数λ1、关联维数D 等，揭示黄河径流的混沌特性。为方便分析，将数据预先做归一化处理。
1.关联维数的计算
采用饱和关联维数（G
P）法求解黄河年径流时间序列的分形维数，取距离半径r范围为[0.06，0.6]，嵌入维数m 在[2，15]内变化，则logC（r）与logr的关系如图6.16所示。可以看出，r从0.2～0.35变化时，对应m为11到14，logC（r）～logr曲线近似为直线，且斜率近似相等。取斜率平均值即可得到黄河年径流序列的关联维数为2.9。
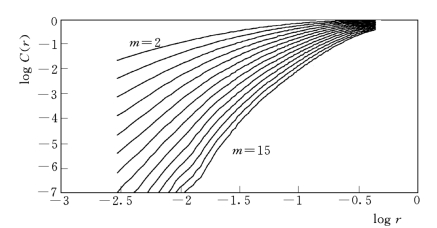
图6.16 年径流关联维数的计算
2.最大Lyapunov指数的计算(www.xing528.com)
取m=7，再令r∈[0.2，0.3]，τ=1，t∈[0，20]，得到S（t）曲线如图6.17所示。可以看出，t从15～20变化，对应不同的半径，曲线有相近的斜率。通过计算斜率平均值，得λ1=0.004。
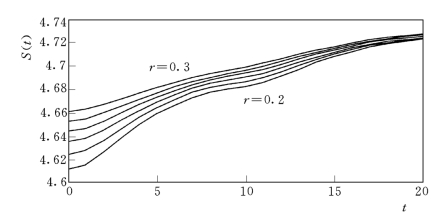
图6.17 年径流最大Lyapunov指数的计算
λ1为正数，D为正小数，表明该序列可能具有混沌特性；λ1值较小，表明该序列的邻近吸引子轨道离散度较低，因此有可能进行较为长期的预测。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
