有限脉冲响应神经网络的学习算法

FIRNN的训练采用一种改进的反向传播算法，称之为“实时算法”。该算法的具体描述如下。

给定单变量输入序列X（t）（t=1，2，…，Tn，Tn为序列点数），假设N[W，X（t）]表示神经网络，Y（t）=N[W，X（t）]为网络产生的输出，其中W 表示网络滤波器系数。假设网络的期望输出为d（t），那么，其实时误差为期望输出和网络输出差值的欧几里得范数的平方，即：e2（t）=‖d（t）—N[W，X（t）]‖2。并通过调整W 使代价函数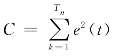最小（Tn为训练样本个数）。通常采用梯度下降法对其进行优化计算。在每一个增量时刻，滤波器可通过式（5.31）更新

式中：为第l层滤波器系数；η表示学习率。

滤波器代价函数的梯度可以扩展为式（5.32）形式

其中，，表示网络输入或者是前一层神经元输出的延时向量。由于神经元的输入在每一个时刻都在变化，可以认为为所有时刻的累积平方误差的变化。因此，式（5.31）可改写为

因此，在每一个增量时刻，滤波器可以通过式（5.34）进行更新(www.xing528.com)

式中

此处，为梯度向量，ej（t）为输出节点的误差，f′（·）为Sigmoid函数的微分，L为神经网络的层数，Nl+1为第l+1层神经元个数。对一个给定的神经元，为了计算δlj（t），可以通过给定神经元输入的脉冲响应的突触过滤下一层的δ，如图5.10所示。

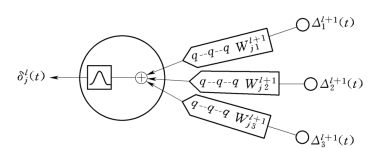
图5.10　δlj（t） 的计算过程

实时反向传播算法既保持了状态的前向传播和误差的后向传播的均匀性，也保存了原有算法并行处理问题的能力。同时，每迭代一次变量只随着网络层数和突触多少而线性增长。