前馈网络在混沌时间序列预测中的应用

使用前馈网络进行混沌时间序列预测的方法是通过前馈神经网络的非线性逼近能力来实现预测原点和预测时域之间的定量关系[2，3，4，23]。假设混沌时间序列通过延迟坐标重构获得如下的延迟坐标向量

式中：m和τ分别为嵌入维数和延迟时间。

假设预测步数为h，需要前馈神经网络来逼近非线性函数

函数Fh可以证明是存在的：由Takens定理[24]可以知道，通过合适地选择嵌入维数m和延迟时间τ，从重构的状态空间中可以无歧义的恢复原系统的吸引子特征。假设在重构的状态空间中状态的演化可以用函数F（·）表示

假设x（t）通过g（·）观测状态向量X（t）

那么有以下式成立

X（t+1）=F[X（t）]

X（t+2）=F[X（t+1）]=F﹛F[X（t）]﹜

⋮

X（t+h）=F[X（t+h—1）]=F﹛…F[X（t）]﹜(www.xing528.com)

x（t+h）=Fh[X（t）]=g（F﹛…F[X（t）]﹜）

以上结论是直接多步预测方法的基础。除此之外，多步预测还可以通过在单步预测器上的迭代操作而形成。具体方法是设置h为1，通过前馈神经网络学习一个较为精确的单步预测器，通过在单步预测器上的迭代操作而形成对不同预测时域的预测。

如图5.4所示为使用前馈网络进行h步直接预测的示意图（不失一般性，设延迟时间τ为1）。从图中可以看出，前馈网络的作用是通过学习样本构建延迟坐标向量X（t）与x（t+h）之间的定量关系。网络训练完毕后，就可以直接进行h步的预测。设置预测时域h为不同的值，可以训练得到不同的神经网络模型，也就是说每一个h需要一个神经网络来逼近。这种情况下网络训练的计算量较大。

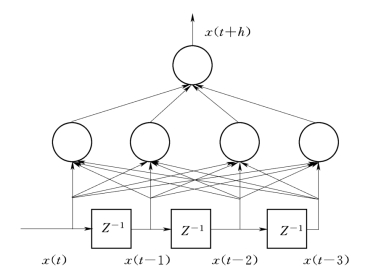
图5.4　前馈网络h步直接预测示意图

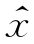多步预测也可以在训练好的单步预测器上进行递推操作完成，如图5.5所示。设置预测步数为1，训练神经网络得到一个单步预测器，从而建立X（t）和x（t+1）之间的定量关系。当神经网络给出一步预测值（t+1）之后，通过预测值（t+1）将预测原点X（t）更新为（t+1），依此类推进行迭代，从而进行多步预测。

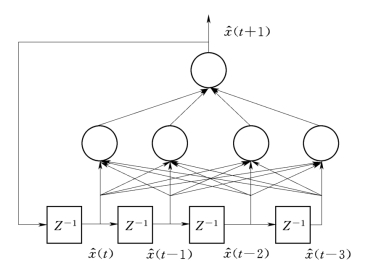
图5.5　基于前馈网络的递推多步预测示意图

图5.5显示的是一种递归神经网络风格的预测模式，网络当前时刻的输出与网络的历史状态有关。但是，在训练过程中，学习算法仍然按照前馈网络的方式。因此，有必要在网络的训练过程中就考虑反馈环的影响，也就是说，把上述的预测问题直接由递归神经网络实现，这个问题将在本章5.6节和5.7节继续讨论。

前馈网络是一类应用的较为广泛的神经网络，最初全局预测方法大多使用前馈神经网络方法。该方法的特点是：

（1）前馈网络实现一种非线性函数的静态逼近，通过延迟坐标窗口与预测时域之间的定量关系建立预测器。

（2）通常情况下预测性能受到网络结构的影响，其中隐含层神经元的个数和正则项系数对预测性能影响较大。