基于序列混沌特性的初始状态选择方法

由于混沌系统对初始条件十分敏感，不同初始条件的混沌演化大相径庭，甚至会影响到混沌现象的产生与否，因此是否合理选择预测初始条件直接影响预测结果的好坏。目前这方面的研究还较为缺乏。一般n维非线性连续时间系统微分方程的表达式为

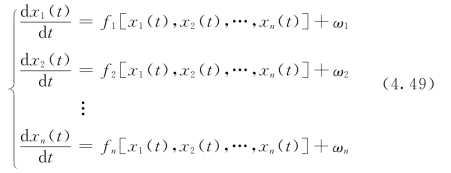
式中：x1，x2，…，xn为描述该系统状态的n个变量；fi（·），i=1，2，…，n，为某种函数关系。

简化上式有

系统输出量测方程为

其中

W、V 分别代表动态白噪声和观测白噪声。利用式（4.50）进行预测时，需要确定系统初始条件，即t=0时，x1（0），x2（0），…，xn（0）的值。

本质上，混沌时间序列预测就是非线性系统时间序列预测，建立在混沌前提下的模型应不包括任何明显的随机成分。如果能够找到反映系统吸引子特性的动态方程，就能精确的表现系统的演化行为。式（4.50）为非线性系统的通用方程。设Xe为邻近X 的点，利用泰勒级数展开，有

式中：g（X）为泰勒级数展开式中二阶及其以上高阶各项之和。

设J（Xe）表示向量函数的Jacobian矩阵：

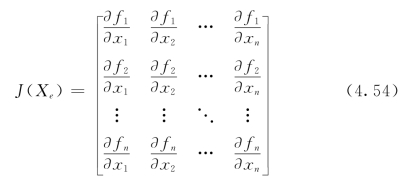
令

通常情况下，可以忽略g（X）。结合式（4.54）和式（4.55），则式（4.53）可线性化为

式（4.56）就是具有一般意义的系统初始模型。在系统相应参数已知的前提下，可以直接将该方程离散化，而后采用相应迭代算法进行自适应预测。但是通常情况下，系统的参数是未知或局部未知的，此时就需应用扩维技术，将系统参数纳入到迭代过程，参与到自适应调整过程中。所以初始模型参数的确定包括两方面的内容：状态变量初始值确定和系统参数初始值确定[61，62]。

1.广义状态向量

以一维映射Logistic方程为例

f（x）=μx（1—x）

图4.3（a）、图4.3（b）分别画出μ=2.8和μ=4时的Logistic序列二维相空间图。f（x）曲线和直线x（t）=x（t+1）的交点为方程的两个不动点，即x（1）=0，x（2）=1—1/μ。以除不动点外的其他点作为初值，任选两个十分靠近的初始值x（01）、x（02），作平行于纵轴的直线与f（x）曲线相交，得到x（11）=f[x（01）]，x（12）=f[x（02）]，在交点处再分别作一平行于横轴的直线又与直线x（t）=x（t+1）相交，两交点的坐标分别对应x（11）和x（12），多次重复上述步骤，迭代过程就会沿着图4.3（a）、图4.3（b）箭头所示途径行进。(www.xing528.com)

分析图4.3（a）的迭代轨迹，可以看出μ=2.8时，不动点x（2）为稳定点，由初值x（01）、x（02）出发的迭代过程终将趋近于x（2）点，系统不表现混沌特性。图4.3（b）中，μ=4，系统由初值x（01）、x（02）出发的迭代过程不趋近于某个不动点，也不发散，而是像分布在区间[0，1]上的随机数，表现出混沌特性。对Logistic映射的分析表明只有参数μ＞3.57时，系统才会出现混沌。因此，在对混沌信号建立初始模型时，参数的选择直接影响系统的内在特性，如果选择不当，将会直接导致预测的失败。另一方面，图4.3（b）中，由x（01）、x（02）出发的两点之间的距离以指数速率分离，这也是混沌特性的一种表现。只有两点初始值足够靠近时，在一定的迭代次数内，其中一点的轨迹才可以作为另一点的近似值，所以状态变量初始值的选择也会对预测精度产生影响。综上所述，引入一个广义状态向量新概念，在确定系统初始模型时，综合考虑系统原有状态向量和系统未知参数的取值。

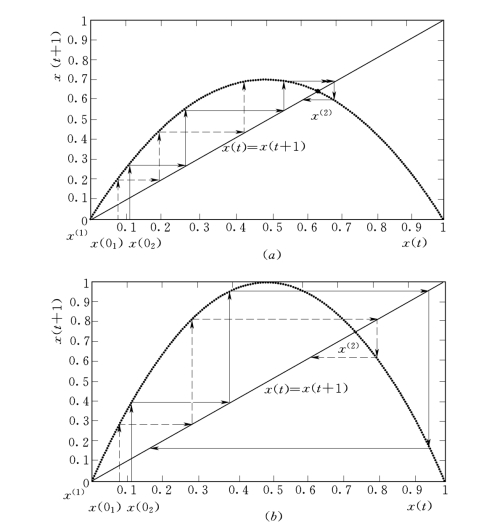
图4.3　Logistic映射相空间

（a）μ=2.8时的Logistic映射相空间；（b）μ=4时的Logistic映射相空间

定义4.1 系统原有状态向量X1和系统未知参数向量X2共同组成的一个扩维向量，称为广义状态向量：

因此，初始模型参数确定需要考虑X1、X2的共同选取，主要遵循以下两个原则：

（1）初始模型演化行为能够表现出与观测序列相似的吸引子结构，如定常吸引子、周期吸引子、奇异吸引子等。

（2）初始模型演化行为能够表现出与观测序列相近的时频参数，包括序列振幅、平均周期等。

原则（1）使得初始模型与观测序列在相空间中的演化规律相似，具有相同的内在特性，即稳定性、周期性、混沌性等。只有二者的内在特性相同，才有可能进行逼近建模；原则（2）则使二者在时域和频域中的演化行为相似，运动范围相近。

2.初始模型参数的确定步骤

满足上述两个原则的初始模型在相空间中将具有和观测序列相似的吸引子轨迹，为精确预测打下良好的基础。初始数学模型选择的步骤如下：

（1）计算所观测序列的混沌特征值，例如奇异吸引子维数、序列振幅、平均周期等。

（2）选择典型的混沌方程，如Rössler、Lorenz方程，其某一状态分量的时间序列能够表现出与所观测时间序列相似的混沌吸引子结构。

（3）通过线性转化，使得典型混沌方程的状态变量时间序列在平均周期和振幅上与观测时间序列近似。例如，令

式中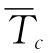：，分别对应观测序列和混沌方程变量序列的平均周期。

用

作为新的时间变量代入典型混沌方程，使得转化后的方程变量序列在t*时间轴上能够与所观测的时间序列保持同步。同理，混沌方程变量序列的振幅也可作相应线性转化，从而可以和所观测时间序列的振幅保持一致。

（4）比较转化后的混沌方程和式（4.56），设置相应参系数的初值。

（5）根据所测的实际数据样本确定状态变量的初值，从而得到整个系统的初始状态。

通过以上步骤确定的系统初始方程，考虑了观测序列的动力学特性，在初始时刻令所建模型在相空间中的演化行为逼近原系统的实际模型，尽可能多的包含系统信息，以改善预测性能。