基于Sigmoid函数的Volterra自适应滤波器的应用

由于各类神经网络如小波网络、模糊神经网络、径向基函数网络、递归神经网络等具有普遍的非线性函数逼近能力，因而它们是用于混沌时间序列预测的主要工具之一。然而对混沌时间序列而言，如果只是用输入—输出对神经网络进行训练，事实上只是调节神经网络去模拟混沌系统行为的某个特定轨迹，即得到的只是给定激励的特定解，当一个新的激励输入系统时，这类预测模型可能得不到正确的系统行为。基于Volterra级数展式的自适应非线性滤波预测模型由于综合利用了线性和非线性项，其本质上属于参数辨识模型，因而较之神经网络对特定的低维混沌序列具有较好的预测能力。但由于二阶Volterra滤波器逼近非线性函数的能力有限，使其在预测高阶混沌序列和时变混沌序列方面有一定的局限性。自适应高阶非线性滤波器在逼近能力方面有较大的提高，能够对包括高维耦合混沌在内的混沌时间序列进行有效地预测。但是这两种自适应非线性滤波预测模型的共同缺点是当输入维数较大时，滤波器的参数呈几何级数增长，使其硬件实现困难。由于神经网络的非线性表达能力来自有界的Sigmoid函数，因此在式（4.34）的基础上，引入Sigmoid函数来构造非线性滤波预测模型，以期提高二阶Volterra预测滤波器的逼近非线性函数和减少待定参数，这种非线性预测滤波器定义如下

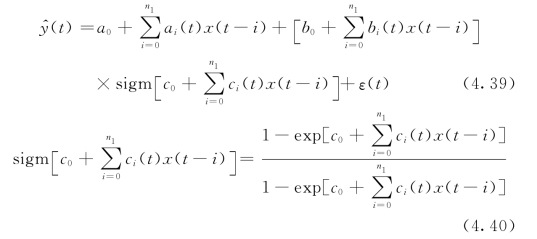
其中，（t）=（t+T）为非线性自适应系统的输出，ε（t）为输出误差，相应的滤波系数总个数为M=3m+3，称式（4.39）与式（4.40）两式描述的非线性模型为基于Sigmoid函数的少参数二次滤波器模型。图4.2给出了相应的实现结构。

图4.2　基于Sigmoid函数的少参数非线性自适应预测滤波器结构

在现有的各种自适应算法中，归一化最小均方（Normalized Least Mean Square，NLMS）自适应算法具有良好的自适应性能，且控制收敛的参数选择范围大，能够直接应用于非线性自适应滤波器。为了使得式（4.39）、式（4.40）能够利用NLMS算法来调整其待定参数，重新定义滤波器的参数和输入向量为

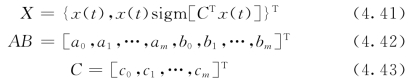(www.xing528.com)

基于最小均方误差准则有

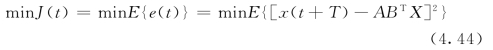
根据归一化的LMS（NLMS）算法，则有

式中：μ1和μ2分别为控制学习收敛的步长参数；ρ=0.1。

由于采用了最优归一化的NLMS自适应算法来自适应地跟踪混沌的运动轨迹而不是重构混沌系统的全局或局部运动轨迹，致使这种基于Sigmoid函数的少参数非线性自适应滤波预测模型能够有效地预测混沌时间序列。