Volterra级数自适应预测模型

理论研究和实践经验表明：实际中大量的非线性系统可用Volterra级数表征。因此可用Volterra级数展开式来构造预测混沌信号的非线性预测模型。

Volterra级数是一种泛函级数，由意大利数学家Volterra于1880年首先提出，当时是作为对Taylor级数的推广而提出的。1912年，Volterra将这种泛函级数用于研究某些积分方程和积分- 微分方程的解。直到1942年，美国著名科学家，控制论的奠基人Wiener才首次将Volterra泛函级数用于非线性系统的分析。后来其他学者继续Wiener的研究工作，将Volterra泛函级数用于发展非线性算子理论以及非线性方程和系统分析。20世纪70年代后Volterra泛函级数开始受到人们的普遍重视。Brockett研究了Volterra级数与几何控制论的关系；美国学者Sandberg利用Volterra级数研究了一大类非线性动力学系统。特别是随着计算机技术的发展，Volterra级数越来越显示出其应用价值与巨大潜力。

Volterra级数理论之所以具有如此大的吸引力，根本原因在于它与幂级数有着天然的密切联系和相似之处，易为广大工程技术人员和科技工作者所接受。Volterra级数具有鲜明的物理意义，对工程技术领域非常切合实际，它不仅提供了一套新的理论，而且为解决非线性实际问题提供了强有力的方法和工具。Volterra级数使得人们能像使用Laplace变换和线性传递函数法分析线性系统那样分析一般的非线性动力学系统，有力地推动和促进了非线性科学的研究与发展。

如前所述，Volterra级数可以描述一大类非线性系统。利用这个特点，可以将Volterra级数用作基于模型的非线性混沌时间序列预测。张家树、肖先赐[10，46，55，56]等人创建了混沌信号非线性自适应预测技术的初步框架，提出并研究了多种非线性自适应预测模型及其自适应预测算法、预测性能。目前，混沌信号的非线性自适应预测法已经广泛应用于通信、图像处理和非线性系统辨识与控制等中。

设非线性离散动力系统的输入为X（n）=[x（n），x（n—1），…，x（n—N+1）]，输出为y（n）=（n+1），则该非线性系统函数的Volterra级数展开式为

式中：hp（m1，m2，…，mp）为p阶Volterra核。

这种无穷级数展开式在实际应用中难以实现，必须采用有限截断和有限求和的形式。最常用的是下面的二阶截断求和的形式：

式（4.32）所示非线性Volterra自适应滤波器可描述成如图4.1所示的结构。

图4.1　Volterra自适应滤波器结构

非线性扩展后的信号为

式中：U（n）为滤波器的输入矢量，且M≥N1，N2。(www.xing528.com)

在实际应用中，滤波器的长度N1、N2应为有限长。对于混沌时间序列，由Takens嵌入定理可知：一个混沌时间序列要完全描述原动力系统的动态行为，至少需要m≥2D2+1个变量，其中D2为关联维数。因此，可将N1、N2均取为N1=N2=m≥2D2+1，则用于混沌序列预测的滤波器为

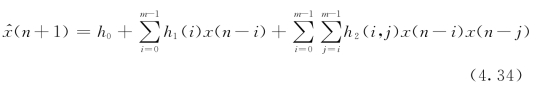
其状态扩展后的系数总个数为M=1+m+m（m+1）/2。

定义线性自适应有限脉冲响应（FIR）滤波器的输入矢量U（n）为

系数向量为

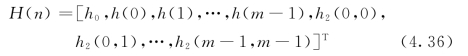
则式（4.34）可表示为

式（4.34）表示的Volterra自适应滤波器的系数可直接利用线性FIR滤波器的自适应算法来确定。对于式（4.37）这种二阶Volterra自适应滤波器，可采用的自适应算法为时间正交（Time Domain Orthogonal，TDO）自适应算法。对于输入矢量U（n），系数矢量H（n），TDO算法可描述如下：

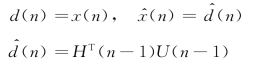
式中：c为控制收敛性能的参数。

二阶Volterra自适应滤波器能够有效地预测低维混沌时间序列的本质在于：Volterra自适应滤波器综合利用线性和非线性的因素，更符合混沌序列的非线性本质。采用Volterra自适应滤波器对混沌时间序列进行预测的另一个优点是它更便于硬件实现，对这种非线性预测滤波器进行深入研究，将有助于它在混沌系统的实时预测方面的应用。