基于局部投影噪声平滑的方法

对不同噪声水平的实际观测序列，常规局部投影噪声平滑方法参数选取如邻域半径、迭代次数等受到人为因素的限制，本小节针对这一问题提出一种优化的局部投影噪声平滑方法[17]。该方法首先对实际观测信号利用二次小波进行噪声水平估计，得到噪声水平初步估计值v作为邻域半径ε，并选择大于和小于该噪声水平的值v1和v2分别作为局部投影噪声平滑方法的邻域半径，应用局部投影方法对实际观测序列进行平滑迭代，除去对应噪声水平的噪声，并得到不同噪声水平的噪声平滑后序列；然后选择现有典型非线性预测方法对不同噪声水平平滑后的序列进行预测，得到对应的预测精确度，并找出使预测精确度最佳的噪声水平；基于优化思想，在此噪声水平值附近必定存在一个最优的值使得噪声平滑后序列的预测精确度最好，从而缩小噪声水平范围，直到找到最佳的噪声水平和噪声平滑序列。该方法的基本步骤如下：

（1）估计噪声水平v，选取v1＜ε＜v2分别作为邻域半径。

（2）用局部投影方法对含噪声信号进行去噪处理。

（3）应用典型预测方法对不同噪声水平平滑后的序列进行预测，得到对应的预测精确度，并对同一序列进行多次预测，计算其平均值，找出使得预测值最佳的噪声水平。预测性能指标可使用均方根误差（RMSE）进行分析，定义如下

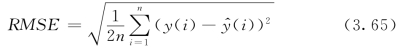
式中：n为预测步数；y为实际序列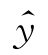值；为预测值。

（4）基于步骤（3）中的最佳噪声水平，缩小范围，重复步骤（2）～步骤（3），直到得到一个最佳的噪声水平值和对应的噪声平滑序列。

该方法的基本流程图如图3.22所示。

图3.22　局部投影噪声平滑的优化方法流程图

仿真数据采用1753年1月至2001年12月的实际观测月太阳黑子时间序列，共2976个，如图3.23所示。

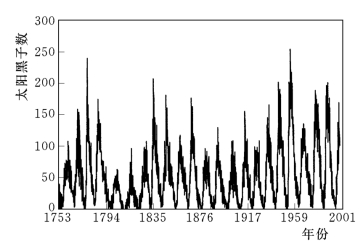
图3.23　实际观测月太阳黑子时间序列

应用二次小波分析方法对月太阳黑子实际观测序列进行噪声水平初始估计，估计值为0.20。为了正确的分析序列，分别取15%、25%、35%的噪声水平，应用局部投影方法分别进行噪声平滑，得到3个噪声平滑后的序列。其中各个参数的选择如下：邻域半径分别选取0.15、0.25、0.35对应着各个不同的噪声水平，嵌入维数为8，最小邻域数35，迭代次数为对应除去该噪声水平的迭代次数。

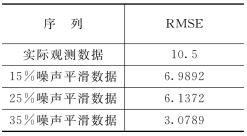
训练和预测使用的是一种标准的前馈神经网络——有限脉冲响应神经网络（Finite Impulse Response Neural Network，FIRNN），该网络最初是由美国斯坦福大学的博士E.Wan[53，54]提出来的。得到的预测结果如表3.2所示：其中预测误差为训练20次后的预测结果的平均值。从表中可以看出，当噪声水平值为35%时，神经网络能够很好学习噪声平滑后混沌时间序列的动态演化特性，得到的预测误差比较小，并且其预测误差是其他噪声水平下预测误差的1/2倍。因此基于优化的思想，最优的噪声水平估计值应该在35%附近，分别选取30%和40%的噪声水平，应用局部投影方法进行噪声平滑，各个参数的选择如下：邻域半径分别选取0.30和0.40对应着各个不同的噪声水平，嵌入维数为8，最小邻域数35，迭代次数为对应除去该噪声水平的迭代次数。

表3.2　实际观测序列和15%、25%、35%噪声水平噪声平滑后序列的预测误差

用同样结构的神经网络分别对30%和40%噪声水平噪声平滑后的序列进行预测，得到如表3.3所示的预测结果。从预测结果可以看出，噪声水平值为35%时的噪声平滑序列预测误差最小，30%为其次，而噪声水平为40%时的噪声平滑序列预测误差最大。这种现象可以解释为：邻域半径越大，噪声平滑算法在相空间中选取的邻域点个数就会越多，当对过多的邻域点进行处理时产生了过修正现象，这种过修正使得原信号中部分有效信息被当做噪声滤除了。因此，神经网络学习到的有用信息减小，从而使得预测精度降低。

表3.3　40%、35%和30%噪声水平噪声平滑后时间序列的预测误差(www.xing528.com)

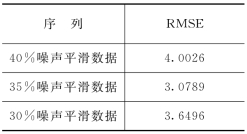
因为噪声水平值为35%时预测误差最小，其次为30%时的预测误差，从优化的角度来看，最优的噪声水平值应该在30%～35%之间。当选择34%噪声水平时，对噪声平滑后的序列用神经网络训练学习并预测，预测误差为2.9456，此时噪声平滑后的序列达到了所有噪声水平预测误差的最小值。根据文献[1]，当噪声水平浮动值在较小的范围内时，比较原噪声对混沌动态特性的影响，其噪声平滑后的序列都是可以接受的。因此，认为仿真所用到的月太阳黑子时间序列最接近的噪声水平为34%。对应的噪声平滑后的序列如图3.24所示。同时分别画出原始观测序列噪声平滑前后的相空间重构图如图3.25（a）和图3.25（b）所示。

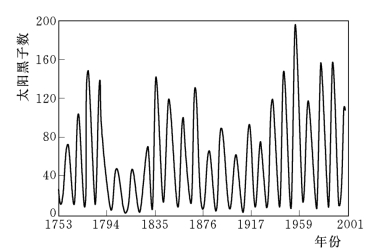
图3.24　34%噪声水平噪声平滑后月太阳黑子序列

图3.25　月太阳黑子相空间重构图

（a）实际观测序列；（b）34%噪声水平噪声平滑后序列

从相空间重构图中可以看出，由于受到噪声的影响，噪声平滑前序列的相图表现为杂乱无章的伪随机性特征，而噪声平滑后的序列展现出清晰而有规律性的混沌吸引子几何结构，表明噪声平滑后混沌序列的内在确定性成分得到了增强。这种光滑的、有规律性的吸引子几何结构充分说明34%噪声水平为实际观测月太阳黑子混沌时间序列的真实接近值，达到了良好的噪声平滑效果，证明该方法对噪声去除的有效性。另外，对34%噪声水平对应的噪声序列和噪声平滑后序列分别进行自相关函数分析，其结果如图3.26（a）和图3.26（b）所示。从图3.26中可以看出，去除部分的自相关度较弱，表现出与随机噪声相似的性能，序列具有不可预测性，而噪声平滑后序列的自相关性得到了增强，充分佐证了除去的部分即为噪声，而噪声平滑后序列为实际月太阳黑子序列。

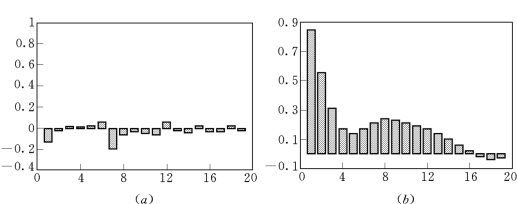
图3.26　自相关函数分析

（a）去除的噪声部分；（b）噪声平滑后序列

同时，对噪声平滑后月太阳黑子进行混沌特性分析，分别计算其关联维数和最大Lyapunov指数。

（1）关联维数。利用前面介绍的计算关联积分和关联指数的方法计算去噪后的太阳黑子数据，得到曲线如图3.27所示。

从图3.27中可以看出，关联指数随着嵌入维数m的增大而增大，且在m=7处达到饱和，得到月太阳黑子的分数维为2.6748，充分说明了月太阳黑子具有一定的低维混沌特性，噪声平滑方法对月太阳黑子数据具有一定的去噪效果。

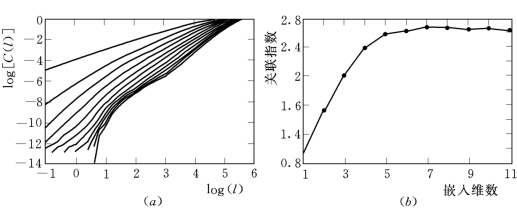
图3.27　月太阳黑子噪声平滑后序列的关联维数结果图

（a）关联积分；（b）关联指数与嵌入维数关系

（2）最大Lyapunov指数。计算噪声平滑后月太阳黑子时间序列的最大Lyapunov指数为0.0772，表明噪声平滑后的序列能够反映月太阳黑子时间序列的混沌特性。