混沌时间序列预测中的子空间维数选取

对于混沌时间序列，用嵌入的方法重构吸引子轨道矩阵X，如果没有噪声或者信噪比很高，则轨道矩阵是奇异的，如果有噪声则轨道矩阵是非奇异的。对轨道矩阵X 进行奇异值分解，可以得到k个非增序列的奇异值s1≥s2≥…≥sk≥0，奇异值的个数与系统有关。记：Si=，则称S1，S2，…，Sk为系统的奇异谱，它表示各个状态变量在整个系统中所占能量的相对关系。一般而言，在系统的奇异谱中只有前面的若干个具有比较大的值，其余的值较小。这些较大的奇异值则对应着信号中的特征成分，而那些比较小的奇异值则对应着信号中的噪声成分。

图3.14为混沌信号和噪声信号的奇异谱图。从图中可以看出，混沌信号和噪声奇异谱明显不同：噪声的奇异谱图较平坦，而混沌信号的奇异谱图有明显的下降趋势。

图3.14　混沌信号和噪声的奇异谱图

局部投影去噪方法的基本思想就是将相空间重构后的向量向q个较大的奇异值对应的特征向量张成的子空间投影，以得到去噪后的时间序列。常规的局部投影方法将每个邻域的投影子空间维数设为固定值，这种方法可以使计算变得比较简单，但是在混沌吸引子中，每个邻域都有自己的动力学特性和几何结构，对所有邻域选取同一个q值便忽略了邻域之间的特殊结构，并且即便是对这个固定的q值，大多数情况下也只能够靠猜想或试验的方法得到，因此很有可能选取的q值不是最能代表吸引子几何结构的q值，固定的q值选取代有一定的主观性。Alexandros Leontitsis等[50]提出了一种动态选取投影子空间维数（即q值）的方法，其思想是通过求取奇异值变化率最大的点作为特征部分和信号部分的分界点，之前的奇异值代表信号的特征部分，之后的奇异值则代表噪声部分。其选取的具体过程如下：对协方差矩阵Ci求取按序排列的特征值s1≥s2≥…≥sm，必定存在一个i，i=1，2，…，m—1，使得si/si+1最大，则i为局部子空间的维数，q=m—i。例如，在一个嵌入维为7维的相空间中，计算协方差矩阵Ci的特征值分布如图3.15（a）所示，则q=5；如果协方差矩阵的特征值分布如图3.15（b）所示，则q=3。(www.xing528.com)

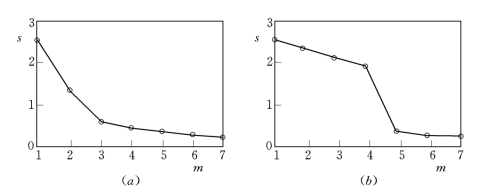
图3.15　q选择示例

（a）q=5；（b）q=3