全局逼近去噪方法:混沌时间序列预测

全局逼近可以通过神经网络来实现，也可以通过径向基函数（Radial Basis Function，RBF）来实现，本书具体介绍利用RBF函数进行全局逼近的思想。

余建祖、苏楠[34]利用RBF函数作为动力学模型的逼近函数，以其作为吸引子轨道的近似函数。仍以Henon映象为例，说明径向基函数近似技术的应用。对Henon映象，由于m=2，因此要找出一个两变量函数F（s，n），在s=x（t），n=x（t—1）对所有的n，其值为x（t+1）。在这个例子中，已知F（s，n）=1—as2+bn（a=1.4，b=0.3），现在假定仅知道采样时序﹛x（t）﹜，而不知道这个函数式。显然，可用三维空间中表面z=F（s，n）来表示F。如果对所有的n值，取时间序列并画出点[s，n，z]=[x（t），x（t—1），x（t+1）]，那么它们将全部落在这个表面上。因此寻求近似函数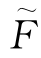即相当于要找到一个通过或接近所有采样点[x（t），x（t—1），x（t+1）]的平滑表面。利用径向基函数方法将这个平面近似为：

式中：﹛x（1），…，x（t）﹜为已知的时序采样值；pt为未知参数；φ（r）为径向基准函数，可取φ（r）=（r2+c）1/2，c是一个大于0的常数。

pt的值可由F[x（t—1），x（t）]=x（t+1）确定，由此得线性矩阵方程为

式中：向量Z=[x2，…，xN]；矩阵ψ的第（i，j）项是ψij=φ（rij），此处rij是点[x（i），x（i—1）]和[x（j），x（j—1）]之间的几何距离；P为矢量P=[p1，…，pN—1]。(www.xing528.com)

可利用解线性方程的标准方法，通过ψ的逆变换，解方程式（3.26）而求出P。在大多数实际应用场合，不大可能获得纯净的混沌信号，而是要处理由混沌时序﹛x（t）﹜和噪声序列﹛w（t）﹜叠加而成的混合信号y（t）=x（t）+w（t），降噪算法可归结为分解混合信号﹛y（t）﹜成2个分量：混沌时序﹛x（t）﹜和噪声序列﹛w（t）﹜，并使﹛w（t）﹜极小化。这可通过“滑动平均数法”（Moving Average）来实现；也可通过“一步预测法”（One Step Prediction）来完成，如对二维系统可通过减小差值F～[y（t）—y（t—1）]—y（t+1）来降低﹛w（t）﹜；或是通过定义一个与状态协方差成比例的畸变矩阵（Distortion Matrix），并找出一个合适的把畸变与噪声幅值换算的规律（Scaling Law），这样通过减小畸变即可降低噪声。

这里采用一步预测并检验误差值et=‖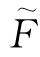[y（t）—y（t—1）]—y（t+1）‖，如果噪声w（t），w（t—1）和w（t+1）的值偏大，则误差值et也偏大；反之，如果w（t）的各项值均是零，en则可忽略不计。进行数值试验的结果也的确如此，因而可由误差﹛et﹜估算噪声﹛w（t）﹜的值。

本方法的降噪效果明显优于传统的线性信号处理技术（如线性自回归和滑动平均数法等）。而且有意义的是，在一定范围内，这种方法的效果是随着混沌时序信噪比的减小而增加的。并且整个径向基准函数的结构及上述降噪方法，可以很方便地扩展到嵌入维m＞2的情况。可从混沌时序构成若干m 维中心点﹛x（t），x（t—τ），…，x[t—（m—1）τ]﹜，而式（3.26）中ψ的自变量r则是想要计算F 值的点与相关中心点之间的距离。